
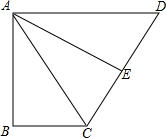
 已知,如图,Rt△ABC中,∠B=90°,AB=6,BC=4,以斜边AC为底边作等腰三角形ACD,腰AD刚好满足AD∥BC,并作腰上的高AE.
已知,如图,Rt△ABC中,∠B=90°,AB=6,BC=4,以斜边AC为底边作等腰三角形ACD,腰AD刚好满足AD∥BC,并作腰上的高AE.分析 (1)由等腰三角形的性质得出∠DAC=∠DCA,由平行线的性质得出∠DAC=∠BCA,得出∠ACB=∠DCA,由AAS证明△ABC≌△AEC,得出AB=AE;
(2)由(1)得:AE=AB=6,CE=CB=4,设DC=x,则DA=x,DE=x-4,由勾股定理得出方程,解方程即可.
解答 (1)证明:∵DA=DC,
∴∠DAC=∠DCA,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠ACB=∠DCA,
又∵AE⊥CD,
∴∠AEC=90°,
∴∠A=∠AEC=90°,
在△ABC和△AEC中,$\left\{\begin{array}{l}{∠B=∠AEC}&{\;}\\{∠ACB=∠DCA}&{\;}\\{AC=AC}&{\;}\\{\;}&{\;}\end{array}\right.$,
∴△ABC≌△AEC(AAS),
∴AB=AE;
(2)解:由(1)得:AE=AB=6,CE=CB=4,
设DC=x,则DA=x,DE=x-4,
由勾股定理得:DE2+AE2=DA2,
即(x-4)2+62=x2,
解得:x=$\frac{13}{2}$,
即CD=$\frac{13}{2}$.
点评 本题考查了等腰三角形的性质、全等三角形的判定与性质、勾股定理;熟练掌握等腰三角形的性质,并能进行推理论证与计算是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| x(g) | 2 | 3 | 4 | 5 | 6 | 7 | … |
| y(cm) | 8.2 | 8.3 | 8.4 | 8.5 | 8.6 | 8.7 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2.9 | B. | 2.9 | C. | -2.8 | D. | 2.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
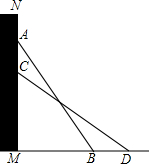 如图,把一个长为10m的梯子AB斜靠在墙上,测得AM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.
如图,把一个长为10m的梯子AB斜靠在墙上,测得AM=8m,BM=6m,梯子沿墙下滑到CD位置,测得∠ABM=∠DCM,求梯子下滑的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com