
分析 (1)根据给定算式,在分式$\frac{1}{\sqrt{7}+\sqrt{6}}$的分母和分子上分别相乘($\sqrt{7}$-$\sqrt{6}$),计算后即可得出结论;
(2)根据给定算式,在分式$\frac{1}{\sqrt{n+1}+\sqrt{n}}$的分母和分子上分别相乘($\sqrt{n+1}$-$\sqrt{n}$),计算后即可得出结论;
(3)根据(2)的结论即可得出$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$=($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+(2-$\sqrt{3}$)+…+(10-$\sqrt{99}$),由此即可算出结论.
解答 解:(1)$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\frac{1×(\sqrt{7}-\sqrt{6})}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}$=$\sqrt{7}$-$\sqrt{6}$;
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{1×(\sqrt{n+1}-\sqrt{n})}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$;
(3)$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{100}+\sqrt{99}}$=($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+(2-$\sqrt{3}$)+…+(10-$\sqrt{99}$)=10-1=9.
点评 本题考查了分母有理化,根据给定算式找出利用平方差公式寻找有理化因式是解题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
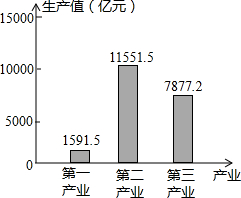 如图是2002年第一季度国内生产总值(亿元)统计图
如图是2002年第一季度国内生产总值(亿元)统计图查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com