练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．方程x2-2x-3=0的根的情况是（　　）
    A．有两个不相等的实数根B．有两个相等的实数根
    C．有且只有一个实数根D．没有实数根

    分析 根据根的判别式得出△=b2-4ac，套入数据求出△的值，由此即可得出结论．

    解答 解：在方程x2-2x-3=0中，
    △=b2-4ac=（-2）2-4×1×（-3）=16＞0，
    故该方程有两个不相等的实数根．
    故选A．

    点评 本题考查了根的判别式，解题的关键是求出b2-4ac的值．本题属于基础题，难度不大，解决该题型题目时，根据根的判别式的正负确定根的个数是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

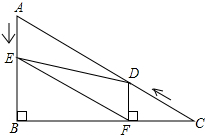    4．如图，在Rt△ABC中，∠B=90°，AC=10，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．
    （1）求证：AE=DF；
    （2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．
    （3）当t为何值时，△DEF为直角三角形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列运算结果正确的是（　　）
    A．$\frac{a}{b}$÷$\frac{c}{d}$=$\frac{ac}{bd}$B．$\frac{b}{a-b}$+$\frac{a}{b-a}$=1
    C．（$\frac{2a}{a-b}$）2=$\frac{4{a}^{2}}{{a}^{2}-{b}^{2}}$D．$\frac{{m}^{4}}{{n}^{5}}$•$\frac{{n}^{4}}{{m}^{3}}$=$\frac{m}{n}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．已知|a+1|+$\sqrt{7+b}$=0，则a+b=（　　）
    A．-8B．-6C．6D．8

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

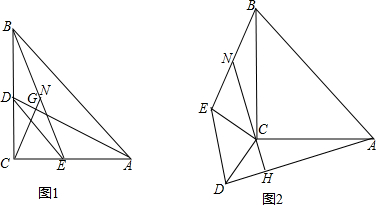
    9．如图，线段MN将长方形纸分成面积相等的两部分，沿MN将这张长方形纸对折后得到图（2），将图（2）沿对称轴对折，得到图（3），已知图（3）所覆盖的面积占长方形纸面积的$\frac{3}{10}$，阴影部分面积为6平方厘米，长方形的面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．二次三项式3x2-2x-6的值为3，则x2-$\frac{2}{3}$x+6的值为（　　）
    A．18B．12C．9D．7

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知x2+x-3=0，求代数式$\frac{{{x^2}-1}}{{{x^2}-2x+1}}•\frac{1}{x+1}+\frac{x+1}{x+2}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．已知$\frac{a}{2}=\frac{b}{3}≠0$，求代数式$\frac{a}{a+2b}-\frac{{4{b^2}}}{{{a^2}+2ab}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图1，在等腰Rt△ACB中，∠ACB=90°，AC=BC，在等腰Rt△DCE中，∠DCE=90°，CD=CE，点D、E分在边BC、AC上，连接AD、BE，点N是线段BE的中点，连接CN，CN与AD交于点G．
    （1）若CN=8.5，CE=8，求S△BDE．
    （2）求证：CN⊥AD．
    （3）把等腰Rt△DCE绕点C转至如图2的位置，点N是线段BE的中点，延长NC交AD于点H，请问（2）中的结论还成立吗？若成立，请给出证明；若不成立，请说明理由．

    查看答案和解析>>

    同步练习册答案