
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E为BC的中点.连接AE,将△ABE沿AE折叠,点B落在点F处,连接CF,现将△CEF绕点E顺时针旋转α角(其中0°≤α≤180°)得到△EC1F1 , 旋转过程中,直线C1F1分别交射线EC、射线AE于点M、N,当EM=EN时,则CM= . 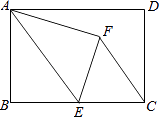
【答案】6﹣ ![]()
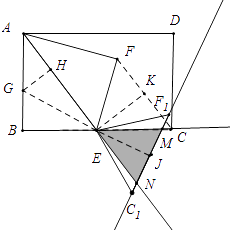
【解析】解:如图作EK⊥FC,EJ⊥MN垂足分别为K、J,延长JE交AB于G,作GH⊥AE垂足为H.
∵四边形ABCD是矩形,AB=8,BC=12,BE=EC
∴∠B=90°,BE=6,AE= ![]() =10,
=10,
∵△AEF是△AEB翻折,
∴∠B=∠AFE=90°,∠BAE=∠EAF,
∴∠BAF+∠BEF=180°,
∵∠BEF+∠FEC=180°,
∴∠FEC=∠BAF,
∵EF=EC,EK⊥FC,
∴∠FEK=∠CEK,
∴∠BAE=∠CEK,
∵∠ABE=∠EKF,
∴△ABE∽△EKF,
∴ ![]() ,即
,即 ![]() ,
,
∴EK= ![]() ,
,
∵△EC1F1是由△EFC旋转,EK⊥FC,EJ⊥F1C1 ,
∴EJ=EK= ![]() ,
,
∵EM=EN,EJ⊥MN,
∴∠MEJ=∠NEJ,
∵∠GEB=∠MEJ,∠GEH=∠NEJ,
∴∠GEB=∠GEH,∵GB⊥BE,GH⊥HE,
∴GB=GH,设GB=GH=x,
在RT△AGH中,由AG2=GH2+AH2 , 得(8﹣x)2=x2+42 ,
∴x=3,
∴BG=GH=3,AG=5,
∴EG= ![]() =,3
=,3 ![]() ,
,
∵∠BEG=∠MEJ,∠B=∠EJM=90°,
∴△EBG∽△EJM,
∴ ![]() ,
,
∴ ![]() ,
,
∴EM= ![]() ,
,
∴CM=EC﹣EM=6﹣ ![]() .
.
所以答案是6﹣ ![]() .
.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点A的坐标为(﹣1,1),AB平行于x轴,则点C的坐标为( ) 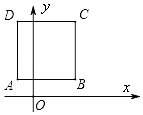
A.(2,5)
B.(3,1)
C.(﹣1,4)
D.(3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中.矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.如果OA=3,OC=2,则经过点E的反比例函数解析式为( ) 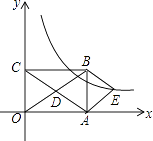
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,四边形ABCD四个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(3,3),D(4,0).
(1)画出四边形ABCD;
(2)把四边形ABCD向下平移4个单位长度,再向左平移2个单位长度得到四边形A′B′C′D′,画出四边形A′B′C′D′,并写出C′的坐标;
(3)求出四边形ABCD的面积.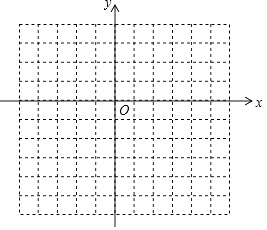
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,PD⊥AB交AB于点D.设运动时间为x(s),△ADP的面积为y(cm2),则y与x的函数图象正确的是( )

A. 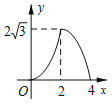 B.
B. 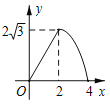 C.
C. 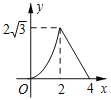 D.
D. 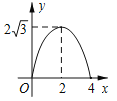
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com