
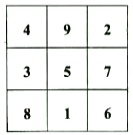
【题目】观察下面3×3的方格中的数据,可以发现每行、每列及对角线上各数之和都相等,我们把这样的图表称为“幻方”.
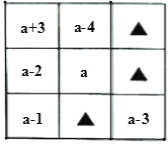
(1)设下面的三阶幻方中间的数字是![]() (其中
(其中![]() 为正整数),请用含
为正整数),请用含![]() 的代数式将下面的幻方填充完整;
的代数式将下面的幻方填充完整;
(2)请你把一4,-3,-2,-1,0,1,2,3,4填入下面3×3的方格中构成幻方.

【答案】(1)见解析;(2)见解析
【解析】
(1)由一条对角线上的三个式子可得每行、每列及对角线上各数之和为3a,根据整式的加减法法则求出表格各式即可;(2)找到按从小到大的顺序排列后正中间的数填在方格的正中间,然后最大的数和最小的数与中间的数进行组合;次大的数和次小的数与中间的数进行组合,依此类推.即可得答案.
(1)∵一条对角线上的三个式子为:a+3,a,a-3,
∴每行、每列及对角线上各数之和为:(a+3)+a+(a-3)=3a,
∴3a-a-(a-1)=a+1,3a-a-(a-2)=a+2,3a-a-(a-4)=a+4,
∴填充表格如下:
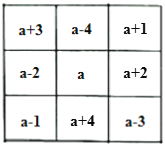
(2)∵中间的一格要被所以有数字加到,所以它取中间值,
∴中间格的数字为0,
∵-1+1=-2+2=-3+3=-4+4=0,
∴填表如下:



 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
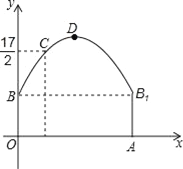
【题目】如图,隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=﹣![]() x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为
x2+bx+c表示,且抛物线的点C到墙面OB的水平距离为3m时,到地面OA的距离为![]() m.
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若代数式(4x2-mx-3y+4)-(8nx2-x+2y-3)的值与字母x的取值无关,求代数式(-m2+2mn-n2)-2(mn-3m2)+3(2n2-mn)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
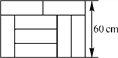
【题目】为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )

A. 当AB=BC时,它是菱形 B. 当AC⊥BD时,它是菱形
C. 当∠ABC=90°时,它是矩形 D. 当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有个填写运算符号的游戏:在“![]() ”中的每个□内,填入
”中的每个□内,填入![]() 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.
(1)计算:![]() ;
;
(2)若请推算![]() □内的符号;
□内的符号;
(3)在“![]() ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
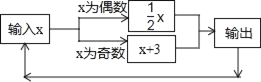
【题目】如图所示的运算程序中,若开始输入的x值为32,我们发现第一次输出的结果为16,第二次输出的结果为8,…,则第2019次输出的结果为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com