
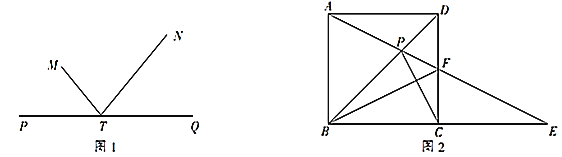
【题目】如图1,直线PQ的同侧有两点M,N,点T在直线PQ上,若∠MTP=∠NTQ,则称点M,N为关于直线PQ的衍射点.如图2,BD是矩形ABCD的对角线,E是边BC延长线上的一点,且CE=BC,连接AE交CD于点F,交BD于点P,连接BF,CP.
(1)求证:点A,B是关于直线CD的衍射点.
(2)若点C,F是关于直线BD的衍射点,CP=2PF=2![]() ,求AB的长.
,求AB的长.
【答案】(1)见解析(2)6
【解析】
(1)由矩形的性质得∠BCD=90°,因为BC=CE,可得FB=FE,故可得∠BFC=∠EFC,,再由∠AFD=∠EFC可得∠AFD=∠BFC进而得到结论;
(2)首先证明△ADF≌△ECF得出F点是DC的中点,再证明△DPF∽△BPA求得![]() ,进而得出AP=CP,再证明△ABP≌△CBP得出AB=BC, 作PQ⊥AB,垂足为点Q,运用勾股定理求出AQ的长以及BQ的长,从而可得AB的长.
,进而得出AP=CP,再证明△ABP≌△CBP得出AB=BC, 作PQ⊥AB,垂足为点Q,运用勾股定理求出AQ的长以及BQ的长,从而可得AB的长.
∵四边形ABCD是矩形,
∴∠BCD=90°,
∵BC=CE,
∴FC垂直平分BE,
∴BF=EF,
∴∠BFC=∠EFC,
∵∠AFD=∠EFC,
∴∠AFD=∠BFC,
∴点A,B是关于直线CD的衍射点;
(2)∵BC=CE,
又∵BC=AD,
∴CE=AD
在△ADF和△ECF中,
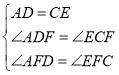
∴△ADF≌△ECF,
∴DF=CF=![]() ,
,
∵DF∥AB,
∴△DPF∽△BPA
∴![]() ,即
,即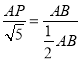
∴![]() ,
,
∵![]() ,
,
∴AP=CP,
又∵点C,F是关于直线BD的衍射点,
∴∠BPC=∠DPF,
∵∠DPF=∠APB,
∴∠BPC=∠APB,
∵AP=PC,BP=BP,
∴△ABP≌△CBP,
∴∠ABP=∠CBP,AB=BC,
又∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABP=![]() ,
,
作PQ⊥AB,垂足为点Q,
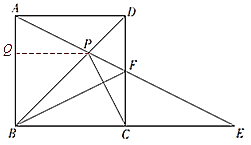
在Rt△BPQ中,BQ=PQ,
设BQ=x,∴PQ=x,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴AQ=![]() x,
x,
在Rt△APQ中,![]() ,
,
∴![]()
解得,![]()
∴BQ=4,AQ=2,
∴AB=BQ+AB=4+2=6.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
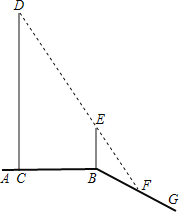
【题目】如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5![]() 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
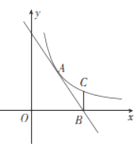
【题目】如图,反比例函数y=![]() (x>0)与直线AB交于点A(2,3),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC交反比例函数的图象于点C,在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,则平行四边形ABCD的面积为____________.
(x>0)与直线AB交于点A(2,3),直线AB与x轴交于点B(4,0),过点B作x轴的垂线BC交反比例函数的图象于点C,在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,则平行四边形ABCD的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=2,点E是边BC的中点,P为AB上一点,连接PE,过点E作PE的垂线交射线AD于点Q,连接PQ,设AP的长为t.
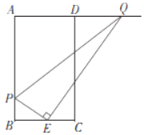
(1)用含t的代数式表示AQ的长;
(2)若△PEQ的面积等于10,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
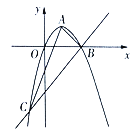
【题目】如图,在平面直角坐标系中,已知抛物线经过原点![]() ,顶点为
,顶点为![]() ,且与直线
,且与直线![]() 相交于
相交于![]() 两点.
两点.
(1)求抛物线的解析式;
(2)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(3)若点![]() 为
为![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴与抛物线交于点
轴与抛物线交于点![]() ,则是否存在以
,则是否存在以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请直接写出点
相似?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过三点(1,0),(-6,0)(0,-3).
的图象经过三点(1,0),(-6,0)(0,-3).
(1)求该二次函数的解析式.
(2)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象在第一象限内交于点A(
的图象在第一象限内交于点A(![]() ),
),![]() 落在两个相邻的正整数之间,请求出这两个相邻的正整数.
落在两个相邻的正整数之间,请求出这两个相邻的正整数.
(3)若反比例函数![]() 的图象与二次函数
的图象与二次函数![]() 的图象在第一象限内的交点为B,点B的横坐标为m,且满足3<m<4,求实数k的取值范围.
的图象在第一象限内的交点为B,点B的横坐标为m,且满足3<m<4,求实数k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.
(1)当吊臂底部A与货物的水平距离AC为5m时,求吊臂AB的长;
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计,计算结果精确到0.1m,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com