
 如图,平行四边形ABCD的对角线相交于点O,OE⊥BD交AD于点E,若BC=10cm,AB=7cm,则△ABE的周长是17cm.
如图,平行四边形ABCD的对角线相交于点O,OE⊥BD交AD于点E,若BC=10cm,AB=7cm,则△ABE的周长是17cm. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}-{b}^{2}}{(a-b)^{2}}=\frac{a+b}{a-b}$ | B. | $\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}=\frac{a-b}{a+b}$ | ||
| C. | $\frac{x-1}{1-{x}^{2}}=\frac{1}{x+1}$ | D. | $\frac{-x-y}{-x+y}=\frac{x-y}{x+y}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
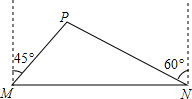 我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com