
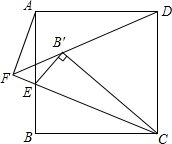
 如图,E为正方形ABCD边AB上的一动点,将△CBE翻折得到△B′CE延长DB′,与CE相交于点F,求AF:B′D.
如图,E为正方形ABCD边AB上的一动点,将△CBE翻折得到△B′CE延长DB′,与CE相交于点F,求AF:B′D. 分析 作CH⊥B′D于H,连接AC,由翻折变换的性质得出∠BCE=∠B′CE,CB′=CD,CH⊥B′D,得出∠B′CH=∠DCH,∠ECH=45°,∠ACF=∠DCH,证出$\frac{FC}{HC}=\frac{AC}{CD}$,得出△AFC∽△HCD,即可得出结果.
解答 证明: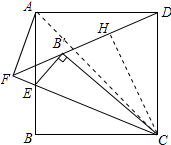 作CH⊥B′D于H,连接AC,如图所示:
作CH⊥B′D于H,连接AC,如图所示:
由翻折变换的性质得:∠BCE=∠B′CE,CB′=CD,CH⊥B′D,
∴∠B′CH=∠DCH,∠ECH=45°,∠ACF=∠DCH,
∴$\frac{FC}{HC}=\sqrt{2}$,
∵$\frac{AC}{CD}=\sqrt{2}$,∠ACF=∠DCH,
∴$\frac{FC}{HC}=\frac{AC}{CD}$,
∴△AFC∽△HCD,
∴$\frac{AF}{DH}=\sqrt{2}$,
∴AF:B′D=$\sqrt{2}$:2.
点评 本题考查了正方形的性质、翻折变换的性质、相似三角形的判定与性质;熟练掌握正方形的性质,证明三角形相似是解决问题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:选择题
| A. | (-2ab)•(-3ab)3=-54a4b3 | B. | (3.5×105)÷(5×106)=7 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (2×108)($\frac{1}{2}$×1016)=1024 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
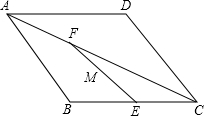 在菱形ABCD中,已知∠ABC=120°,BC=6cm,点E是BC边的中点,F是对角线AC上任意点,现有动点M从点E出发,沿在线段E→F→A移动,在线段EF上的移动速度是1cm/s,在线段FA上的速度是2cm/s,则点M从E到A所需时间的最小值是3$\sqrt{3}$秒.
在菱形ABCD中,已知∠ABC=120°,BC=6cm,点E是BC边的中点,F是对角线AC上任意点,现有动点M从点E出发,沿在线段E→F→A移动,在线段EF上的移动速度是1cm/s,在线段FA上的速度是2cm/s,则点M从E到A所需时间的最小值是3$\sqrt{3}$秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
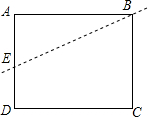 如图,矩形纸片ABCD,AB=10,BC=7,点E在边AD上,沿直线BE折叠纸片,当A对应点A1到边DC的距离为1时,则AE=$\frac{10}{3}$.
如图,矩形纸片ABCD,AB=10,BC=7,点E在边AD上,沿直线BE折叠纸片,当A对应点A1到边DC的距离为1时,则AE=$\frac{10}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com