
【题目】如图,在等边三角形ABC中,D为AC的中点,![]() ,则和△AED(不包含△AED)相似的三角形有( )
,则和△AED(不包含△AED)相似的三角形有( )
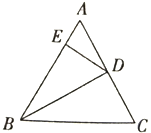
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
由于△ABC是等边三角形,那么可知其三边相等,三个内角相等,再根据D是AC中点,以及AEEB=13,易得AE:AD=1:2=AD:AB,而∠A=∠A,可证△AED∽△ADB,同理可证△AED∽△CDB.
∵△ABC是等边三角形,
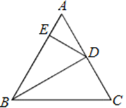
∴AB=AC=BC,
又∵D是AC中点,
∴BD⊥AC,∠ABD=30°,AD:AC=1:2,
∵![]() ,
,
∴AE:AB=1:4,
∴AE:AD=1:2=AD:AB,
又∵∠A=∠A,
∴△AED∽△ADB,
∴∠AED=∠ADB=90°.
∵∠A=∠C=60°,CD:BC=AE:AD=1:2,
∴△AED∽△CDB.
∵∠AED=∠DEB=90°,∠ADE=∠DBE=30°,
∴△AED∽DEB.
故选C.


科目:初中数学 来源: 题型:
【题目】超市购买大件物品都有送货上门服务,那么罗平沃尔玛超市一辆货车从超市出发,向东走了![]() ,到达小明家,继续向东走了
,到达小明家,继续向东走了![]() 到达小红家,又向西走了
到达小红家,又向西走了![]() 到达小英家,最后回到超市.
到达小英家,最后回到超市.
(1)请以超市为原点,以向东为正方向,用1个单位长度表示![]() ,画出数轴.并在数轴上表示出小明家、小红家、小英家的位置;
,画出数轴.并在数轴上表示出小明家、小红家、小英家的位置;
(2)小英家距小明家有多远?
(3)货车一共行驶了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,作AB边的垂直平分线交直线BC于M,交AB于点N.
,作AB边的垂直平分线交直线BC于M,交AB于点N.

(1)如图![]() ,若
,若![]() ,则
,则![]() =_________度;
=_________度;
(2)如图![]() ,若
,若![]() ,则
,则![]() =_________度;
=_________度;
(3)如图![]() ,若
,若![]() ,则
,则![]() =________度;
=________度;
(4)由![]() 问,你能发现
问,你能发现![]() 与∠A有什么关系?写出猜想,并证明。
与∠A有什么关系?写出猜想,并证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=AC,P为斜边BC上一点(PB<CP),分别过点B,C作BE⊥AP于点E,CD⊥AP于点D.
(1)求证:AD=BE;
(2)若AE=2DE=2,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC的三边长分别为6 cm、7.5 cm、9 cm,三角形DEF的一边长为4 cm.当三角形DEF的另两边长是下列哪一组时,这两个三角形相似( )
A. 2 cm、3 cm B. 4 cm、5 cm C. 5 cm、6 cm D. 6 cm、7 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD、BE为高,AN为角平分线,OM平分∠BOC交BC于M.
(1) 若∠BAC=![]() ,求∠BOM;
,求∠BOM;
(2) 求证: OM∥AN.
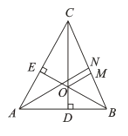
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,马戏团让狮子和公鸡表演跷跷板节目.跷跷板支柱 AB的高度为1.2米.
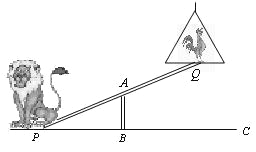
(1)若吊环高度为2米,支点 A为跷跷板 PQ的中点,狮子能否将公鸡送到吊环上?为什么?
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点 A移到跷跷板 PQ的什么位置时,狮子刚好能将公鸡送到吊环上?
查看答案和解析>>
科目:初中数学 来源: 题型:
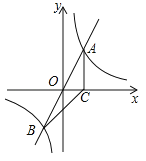
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
(1)求k的值;
(2)x轴上是否存在一点D,使△ABD为直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实现营养套餐的合理搭配,某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮.甲种袋装粗粮每袋含有3千克A粗粮,1千克B粗粮,1千克C粗粮;乙种袋装粗粮每袋含有1千克A粗粮,2千克B粗粮,2千克C粗粮.甲、乙两种袋装粗粮每袋成本分别等于袋中的A、B、C三种粗粮成本之和.已知每袋甲种粗粮的成本是每千克A种粗粮成本的7.5倍,每袋乙种粗粮售价比每袋甲种粗粮售价高20%,乙种袋装粗粮的销售利润率是20%.当销售这两款袋装粗粮的销售利润率为24%时,该电商销售甲、乙两种袋装粗粮的袋数之比是_____(商品的销售利润率=![]() ×100%)
×100%)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com