
分析 (1)方程有两个不相等的实数根,则判别式大于0,据此即可列不等式求得k的范围;
(2)利用根与系数的关系,说明两根的和小于0,且两根的积大于0即可;
(3)不妨设A(x1,0),B(x2,0).利用x1,x2表示出OA、OB的长,则根据根与系数的关系,以及OA+OB=OA•OB即可列方程求解.
解答 解:(1)∵方程x2+(2k+1)x+k2+1=0有两个不相等实数根
∴△=(2k+1)2-4(k2+1)>0,
∴k>$\frac{3}{4}$;
(2)∵x1、x2是方程x2+(2k+1)x+k2+1=0的两个不相等实数根,且k>$\frac{3}{4}$,
∴x1+x2=-(2k+1)<0,
x1•x2=k2+1>0,
∴x1<0,x2<0,
(3)∵x1<0,x2<0
∴OA+OB=|x1|+|x2|=-x1-x2=-(x1+x2)=2k+1,
OA•OB=-x1•(-x2)=x1•x2,
∴2k+1=k2+1,
整理得k2+2k=0,
∴k1=0,k2=2,
又∵k>$\frac{3}{4}$,
∴k=2.
点评 本题考查了二次函数与x轴的交点,两交点的横坐标就是另y=0,得到的方程的两根,则满足一元二次方程的根与系数的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
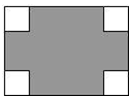 如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.
如图,在长为10cm,宽为8cm的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,则所截去小正方形的边长是2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
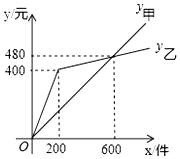 某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售量x(单位:件)的函数关系如图所示,请你根据图象解决下列问题:
某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售量x(单位:件)的函数关系如图所示,请你根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
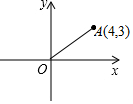 如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有( )个.
如图,在直角坐标系中,O是原点,已知A(4,3),P是坐标轴上的一点,若以O、A、P三点组成的三角形为等腰三角形,则满足条件的点P共有( )个.| A. | 4个 | B. | 6个 | C. | 8个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com