
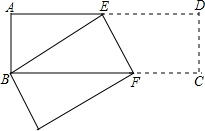
 如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为6cm2.
如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为6cm2. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:一次越野赛中,当小明跑了1600米时,小强跑了1400米.小明,小强此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示.
已知:一次越野赛中,当小明跑了1600米时,小强跑了1400米.小明,小强此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 杀伤半径 | 20≤x<40 | 40≤x<60 | 60≤x<80 | 80≤x<100 |
| 数量 | 8 | 12 | 25 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com