Question

12．如图1，已知A（a，0），B（0，b）分别为两坐标轴上的点，且a、b满足（a-b）²+$\sqrt{b-6}$=0，OC：OA=1：3．
（1）求A、B、C三点的坐标；
（2）若D（1，0），过点D的直线分别交AB、BC于 E、F两点，设 E、F两点的横坐标分别为x_E、x_F．当BD平分△BEF的面积时，求 x_E+x_F 的值；
（3）如图2，若M（2，4），点P是x轴上A点右侧一动点，AH⊥PM于点H，在HM 上取点G，使HG=HA，连接CG，当点P在点A右侧运动时，∠CGM的度数是否改变？若不变，请求其值；若改变，请说明理由．

Answer 1

分析 （1）由偶次方和算术平方根的非负性质求出a和b的值，得出点A、B的坐标，再求出OC，即可得出点C的坐标；
（2）作EG⊥x轴于G，FH⊥x轴于H，由三角形的面积关系得出DF=DE，由AAS证明△FDH≌△EDG，得出DH=DG，即可得出结果；
（3）作MQ⊥x轴于Q，连接CM、AG、M，证出△MCQ是等腰直角三角形，得出∠MCQ=45°，同理：△MPQ是等腰直角三角形，∠MAQ=45°，△AHG是等腰直角三角形，得出∠AGH=45°=∠MCQ，证出A、G、M、C四点共圆，由圆周角定理即可得出结论．

解答 解：（1）∵（a-b）²+$\sqrt{b-6}$=0，
∴a-b=0，b-6=0，
∴a=b=6，
∴A（6，0），B（0，6），
∴OA=OB=6，
∵OC：OA=1：3．
∴OC=2，
∴C（-2，0）；
（2）作EG⊥x轴于G，FH⊥x轴于H，如图1所示：
则∠FHD=∠EGD=90°，
∵BD平分△BEF的面积，
∴DF=DE，
在△FDH和△EDG中，$\left\{\begin{array}{l}{∠FHD=∠EGD}&{\;}\\{∠FDH=∠EDG}&{\;}\\{DF=DE}&{\;}\end{array}\right.$，
∴△FDH≌△EDG（AAS），
∴DH=DG，即-x_E+1=x_F，-1，
∴x_E+x_F=2；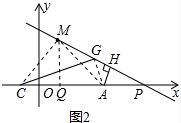
（3）∠CGM的度数不改变，∠CGM=45°；
理由如下：作MQ⊥x轴于Q，连接CM、AG、M，如图2所示：
则MQ=4，OQ=2，
∴CQ=2+2=4，
∴△MCQ是等腰直角三角形，
∴∠MCQ=45°，∵
同理：△MQA是等腰直角三角形，
∴∠MAQ=45°，
∵AH⊥PM，HG=HA，
∴△AHG是等腰直角三角形，
∴∠AGH=45°=∠MCQ，
∴A、G、M、C四点共圆，
∴∠CGM=∠MAQ=45°．

点评 本题是三角形综合题目，考查了偶次方和算术平方根的非负性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、四点共圆、圆周角定理等知识；熟练掌握全等三角形的判定与性质、证明三角形是等腰直角三角形和四点共圆是解决问题的关键．