
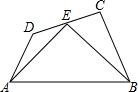
 如图,在四边形ABCD中,∠BCD=90°,E为CD的中点,连接AE、BE,AE=BE,AE⊥BE,若BC-CD=2,AD=$\sqrt{74}$,则AB边的长为13$\sqrt{2}$.
如图,在四边形ABCD中,∠BCD=90°,E为CD的中点,连接AE、BE,AE=BE,AE⊥BE,若BC-CD=2,AD=$\sqrt{74}$,则AB边的长为13$\sqrt{2}$. 分析 过A作AF⊥CD于点F,首先证明△AFE≌△ECB,设CE=x,则AF=DE=x,CD=2x,则EF=BC=2x+2,DF=EF-DE=2x+2-x=x+2
在Rt△ADF中,x2+(x+2)2=($\sqrt{74}$)2,在Rt△AEF中,根据AE=$\sqrt{A{F}^{2}+E{F}^{2}}$求出AE,再根据AB=$\sqrt{2}$AE,即可解决问题.
解答 解:过A作AF⊥CD于点F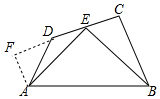
∵∠F=∠AEB=∠C=90°,
∴∠AEF+∠FAD=90°,∠AEF+∠CEB=90°,
∴∠FAE=∠CEB,
在△AFE和△ECB中,
$\left\{\begin{array}{l}{∠F=∠C}\\{∠FAE=∠CEB}\\{AE=EB}\end{array}\right.$,
∴△AFE≌△ECB
∴AF=CE,EF=BC
∵E是CD中点,
∴DE=EC
∵BC-CD=2,
∴BC=CD+2
设CE=x,则AF=DE=x,CD=2x,EF=BC=2x+2
DF=EF-DE=2x+2-x=x+2
在Rt△ADF中,x2+(x+2)2=($\sqrt{74}$)2
∴x=5
在Rt△AEF中,AE=$\sqrt{A{F}^{2}+E{F}^{2}}$=13,
∴AB=$\sqrt{2}$AE=13$\sqrt{2}$,
故答案为13$\sqrt{2}$
点评 本题考查全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,灵活运用勾股定理,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -8 | +14 | -10 | +15 | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
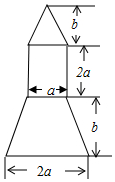 2016年10月17日7时30分,神舟十一号飞船顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图示是火箭模型的截面图,下面是等腰梯形,中间是长方形,上面是一个等腰三角形.
2016年10月17日7时30分,神舟十一号飞船顺利升空,同学们倍受鼓舞,开展了火箭模型制作比赛,如图示是火箭模型的截面图,下面是等腰梯形,中间是长方形,上面是一个等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com