
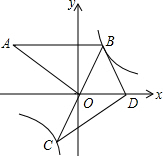
 如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=$\frac{k}{x}$经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=$\frac{k}{x}$经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.分析 (1)先求得△BOD是等边三角形,即可求得B的坐标,然后根据待定系数法即可求得双曲线的解析式;
(2)求得OB=OC,即可求得C的坐标,根据C的坐标即可判定点C是否在双曲线上.
解答 解:(1)∵AB∥x轴,
∴∠ABO=∠BOD,
∵∠ABO=∠CBD,
∴∠BOD=∠OBD,
∵OB=BD,
∴∠BOD=∠BDO,
∴△BOD是等边三角形,
∴∠BOD=60°,
∴B(1,$\sqrt{3}$);
∵双曲线y=$\frac{k}{x}$经过点B,
∴k=1×$\sqrt{3}$=$\sqrt{3}$.
∴双曲线的解析式为y=$\frac{\sqrt{3}}{x}$.
(2)∵∠ABO=60°,∠AOB=90°,
∴∠A=30°,
∴AB=2OB,
∵AB=BC,
∴BC=2OB,
∴OC=OB,
∴C(-1,-$\sqrt{3}$),
∵-1×(-$\sqrt{3}$)=$\sqrt{3}$,
∴点C在双曲线上.
点评 本题考查了反比例函数图象上点的坐标特征,旋转的性质,等边三角形的判定和性质,待定系数法求二次函数的解析式等,求得△BOD是等边三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 至少有1个球是黑球 | B. | 至少有1个球是白球 | ||
| C. | 至少有2个球是黑球 | D. | 至少有2个球是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
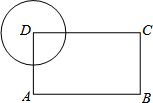 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是3<r<5.
如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是3<r<5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
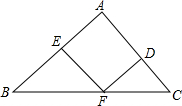 如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD=( )
如图,在△ABC中,点D、E、F分别是三条边上的点,EF∥AC,DF∥AB,∠B=45°,∠C=60°.则∠EFD=( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了治理大气污染,我国中部某市抽取了该市2014年中120天的空气质量指数,绘制了如下不完整的统计图表:空气质量指数统计表
为了治理大气污染,我国中部某市抽取了该市2014年中120天的空气质量指数,绘制了如下不完整的统计图表:空气质量指数统计表 | 级别 | 指数 | 天数 | 百分比 |
| 优 | 0-50 | 24 | m |
| 良 | 51-100 | a | 40% |
| 轻度污染 | 101-150 | 18 | 15% |
| 中度污染 | 151-200 | 15 | 12.5% |
| 重度污染 | 201-300 | 9 | 7.5% |
| 严重污染 | 大于300 | 6 | 5% |
| 合计 | 120 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com