
°æƒø°ø≈◊ŒÔœflC1£∫y1=mx2©Å4mx+2n©Å1”Î∆Ω––”⁄x÷·µƒ÷±œflΩª”⁄A°¢B¡Ωµ„£¨«“Aµ„◊¯±ÍŒ™£®©Å1£¨2£©£¨«ÎΩ·∫œÕºœÛ∑÷Œˆ“‘œ¬Ω·¬€£∫¢Ÿ∂‘≥∆÷·Œ™÷±œflx=2£ª¢⁄≈◊ŒÔœfl”Îy÷·Ωªµ„◊¯±ÍŒ™£®0£¨©Å1£©£ª¢€m£æ![]() £ª¢‹»Ù≈◊ŒÔœflC2£∫y2=ax2£®a°Ÿ0£©”Îœfl∂ŒAB«°”–“ª∏ˆπ´π≤µ„£¨‘Úaµƒ»°÷µ∑∂Œß «
£ª¢‹»Ù≈◊ŒÔœflC2£∫y2=ax2£®a°Ÿ0£©”Îœfl∂ŒAB«°”–“ª∏ˆπ´π≤µ„£¨‘Úaµƒ»°÷µ∑∂Œß «![]() °‹a£º2£ª¢›≤ªµ» Ωmx2©Å4mx+2n£æ0µƒΩ‚◊˜Œ™∫Ø ˝C1µƒ◊‘±‰¡øµƒ»°÷µ ±£¨∂‘”¶µƒ∫Ø ˝÷µæ˘Œ™’˝ ˝£¨∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝”–£® £©
°‹a£º2£ª¢›≤ªµ» Ωmx2©Å4mx+2n£æ0µƒΩ‚◊˜Œ™∫Ø ˝C1µƒ◊‘±‰¡øµƒ»°÷µ ±£¨∂‘”¶µƒ∫Ø ˝÷µæ˘Œ™’˝ ˝£¨∆‰÷–’˝»∑Ω·¬€µƒ∏ˆ ˝”–£® £©
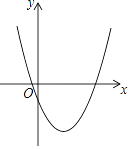
A. 2∏ˆ B. 3∏ˆ C. 4∏ˆ D. 5∏ˆ
°æ¥∞∏°øB
°æΩ‚Œˆ°ø
∏˘æ›≈◊ŒÔœflµƒ∂‘≥∆÷·÷±œflπ´ Ω£¨º¥ø…«Ûµ√∂‘≥∆÷·÷±œfl£ª∏˘æ›≈◊ŒÔœfl”Î◊¯±Í÷·µƒΩªµ„µƒ◊¯±ÍÃÿµ„£¨µ√≥ˆCµ„µƒ◊¯±ÍŒ™£∫£®0£¨2n-1£©;∞—Aµ„◊¯±Í£®-1.2£©¥˙»Î≈◊ŒÔœflΩ‚Œˆ Ω£¨’˚¿Ìµ√:2n=3-5m,‘Ÿ¥˙»Î![]() £¨’˚¿Ìµ√£∫
£¨’˚¿Ìµ√£∫![]()
”…“—÷™≈◊ŒÔœfl”Îx÷·”–¡Ω∏ˆΩªµ„£¨π ∆‰∏˘µƒ≈–± Ω”¶∏√¥Û”⁄0£¨¥”∂¯¡–≥ˆπÿ”⁄mµƒ≤ªµ» Ω£¨Ω‚≥ˆmµƒ»°÷µ∑∂Œß£ª”…≈◊ŒÔœflµƒ∂‘≥∆–‘£¨Bµ„µƒ◊¯±ÍŒ™B£®5£¨2£©£¨µ±![]() µƒÕºœÒ∑÷±π˝µ„A°¢B ±£¨∆‰”Îœfl∂Œ∑÷±”–«“÷ª”–“ª∏ˆπ´π≤µ„£¨¥À ±£¨aµƒ÷µ∑÷±Œ™
µƒÕºœÒ∑÷±π˝µ„A°¢B ±£¨∆‰”Îœfl∂Œ∑÷±”–«“÷ª”–“ª∏ˆπ´π≤µ„£¨¥À ±£¨aµƒ÷µ∑÷±Œ™![]() ,¥”∂¯µ√≥ˆaµƒ»°÷µ∑∂Œß£ª≤ªµ» Ω
,¥”∂¯µ√≥ˆaµƒ»°÷µ∑∂Œß£ª≤ªµ» Ω![]() µƒΩ‚ø…“‘ø¥◊˜ «£¨≈◊ŒÔœfl
µƒΩ‚ø…“‘ø¥◊˜ «£¨≈◊ŒÔœfl![]() Œª”⁄÷±œfly=-1…œ∑Ωµƒ≤ø∑÷£¨‘Ú¥À ±xµƒ»°÷µ∑∂Œß∞¸∫¨‘⁄
Œª”⁄÷±œfly=-1…œ∑Ωµƒ≤ø∑÷£¨‘Ú¥À ±xµƒ»°÷µ∑∂Œß∞¸∫¨‘⁄![]() ∫Ø ˝÷µ∑∂Œß÷ƃ⁄£¨»ª∫Û◊˜≥ˆ≈–∂œº¥ø….
∫Ø ˝÷µ∑∂Œß÷ƃ⁄£¨»ª∫Û◊˜≥ˆ≈–∂œº¥ø….
¢Ÿ≈◊ŒÔœflµƒ∂‘≥∆÷·Œ™÷±œfl![]() £¨π ¢Ÿ’˝»∑£ª
£¨π ¢Ÿ’˝»∑£ª
¢⁄µ±x=0 ±£¨y=2n-1,π ¢⁄¥ÌŒÛ£ª
¢€ ∞—Aµ„◊¯±Í£®-1.2£©¥˙»Î≈◊ŒÔœflΩ‚Œˆ Ω£¨’˚¿Ìµ√:2n=3-5m
‘Ÿ¥˙»Î![]() £¨’˚¿Ìµ√£∫
£¨’˚¿Ìµ√£∫![]()
”…“—÷™≈◊ŒÔœfl”Îx÷·”–¡Ω∏ˆΩªµ„£¨‘Ú
![]() £¨’˚¿Ìµ√:
£¨’˚¿Ìµ√:![]()
Ω‚µ√£∫m>![]() £¨π ¢€¥ÌŒÛ.
£¨π ¢€¥ÌŒÛ.
¢‹”…≈◊ŒÔœflµƒ∂‘≥∆–‘£¨Bµ„µƒ◊¯±ÍŒ™B£®5£¨2£©
∆‰”Îœfl∂Œ∑÷±”–«“÷ª”–“ª∏ˆπ´π≤µ„
¥À ±£¨aµƒ÷µ∑÷±Œ™![]()
µ√≥ˆaµƒ»°÷µ∑∂Œß,º¥![]() £¨π ¢‹’˝»∑.
£¨π ¢‹’˝»∑.
¢›≤ªµ» Ω![]() µƒΩ‚◊˜Œ™∫Ø ˝C1µƒ◊‘±‰¡øµƒ»°÷µ ±£¨∂‘”¶µƒ∫Ø ˝÷µæ˘Œ™’˝ ˝,π ¢›’˝»∑,π —°B.
µƒΩ‚◊˜Œ™∫Ø ˝C1µƒ◊‘±‰¡øµƒ»°÷µ ±£¨∂‘”¶µƒ∫Ø ˝÷µæ˘Œ™’˝ ˝,π ¢›’˝»∑,π —°B.


 »´”≈øºµ‰µ•‘™ºÏ≤‚æ̺∞πÈ¿‡◊‹∏¥œ∞œµ¡–¥∞∏
»´”≈øºµ‰µ•‘™ºÏ≤‚æ̺∞πÈ¿‡◊‹∏¥œ∞œµ¡–¥∞∏ ∆∑—ßÀ´”≈æÌœµ¡–¥∞∏
∆∑—ßÀ´”≈æÌœµ¡–¥∞∏ –°—ß∆⁄ƒ©≥Â¥Ã100∑÷œµ¡–¥∞∏
–°—ß∆⁄ƒ©≥Â¥Ã100∑÷œµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒABCDµƒ±fl≥§Œ™4£¨µ„E «ABµƒ÷–µ„£¨µ„P¥”µ„E≥ˆ∑¢£¨—ÿ![]() “∆∂Ø÷¡÷’µ„C.…˵„Pæ≠π˝µƒ¬∑æ∂≥§Œ™x£¨
“∆∂Ø÷¡÷’µ„C.…˵„Pæ≠π˝µƒ¬∑æ∂≥§Œ™x£¨![]() µƒ√ʪ˝Œ™y£¨‘Úœ¬¡–ÕºœÛƒ‹¥Û÷¬∑¥”≥y”Îx÷ƺ‰µƒ∫Ø ˝πÿœµµƒ «£® £©
µƒ√ʪ˝Œ™y£¨‘Úœ¬¡–ÕºœÛƒ‹¥Û÷¬∑¥”≥y”Îx÷ƺ‰µƒ∫Ø ˝πÿœµµƒ «£® £©
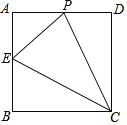
A.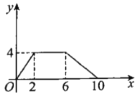 B.
B.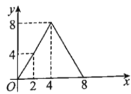
C.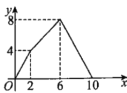 D.
D.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™Ã·–—»À√«Ω⁄‘º”√ÀÆ£¨º∞ ±–fi∫√¬©ÀƵƒÀÆ¡˙Õ∑£Æ–°√˜Õ¨—ß◊ˆ¡ÀÀÆ¡˙Õ∑¬©ÀÆ µ—È£¨√ø∏Ù10√Îπ€≤Ï¡øÕ≤÷–ÀƵƒÃª˝£¨º«¬ºµƒ ˝æ›»Á±Ì£®¬©≥ˆµƒÀÆ¡øæ´»∑µΩ1∫¡…˝£©£¨“—÷™”√”⁄Ω”ÀƵƒ¡øÕ≤◊Ó¥Û»›¡øŒ™100∫¡…˝£Æ
±º‰t£®√Σ© | 10 | 20 | 30 | 40 | 50 | 60 | 70 |
¡øÕ≤ƒ⁄ÀÆ¡øv£®∫¡…˝£© | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
£®1£©‘⁄Õº÷–µƒ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“‘£®t,v£©Œ™◊¯±Í√Ë≥ˆ…œ±Ì÷– ˝æ›∂‘”¶µƒµ„£ª
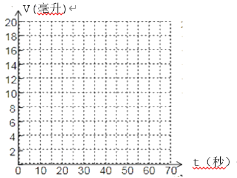
£®2£©”√π‚ª¨µƒ«˙œfl¡¨Ω”∏˜µ„£¨ƒ„≤¬≤‚V”Îtµƒ∫Ø ˝πÿœµ Ω «______________£Æ
£®3£©Ω‚戌 £∫
¢Ÿ–°√˜Õ¨—ßÀ˘”√¡øÕ≤ø™ º µ—È«∞‘≠”–¥ÊÀÆ ∫¡…˝£ª
¢⁄»Áπ˚–°√˜Õ¨—ߺÖ¯ µ—È£¨µ±¡øÕ≤÷–µƒÀÆ∏’∫√ ¢¬˙ ±£¨À˘–Ë ±º‰ «_____√Σª
¢€∞¥¥À¬©ÀÆÀŸ∂»£¨∞Ζ° ±ª·¬©ÀÆ ∫¡…˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™«Ï◊£2015ƒÍ‘™«“µƒµΩ¿¥£¨—ß–£æˆ∂®æŸ––°∞«Ï‘™µ©”≠–¬ƒÍ°±Œƒ“’—›≥ˆ£¨∏˘æ›—›≥ˆ–Ë“™£¨”√700‘™π∫Ω¯º◊°¢““¡Ω÷÷ª® ¯π≤260∂‰£¨∆‰÷–º◊÷÷ª® ¯±»““÷÷ª® ¯…Ÿ”√100‘™£¨“—÷™º◊÷÷ª® ¯µ•º€±»““÷÷ª® ¯µ•º€∏fl20%£¨““÷÷ª® ¯µƒµ•º€ «∂‡…Ÿ‘™?º◊°¢““¡Ω÷÷ª® ¯∏˜π∫¬Ú¡À∂‡…Ÿ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™![]() £¨µ„
£¨µ„![]() °¢
°¢![]() °¢
°¢![]() °¢°≠‘⁄…‰œflON…œ£¨µ„
°¢°≠‘⁄…‰œflON…œ£¨µ„![]() °¢
°¢![]() °¢
°¢![]() °¢°≠‘⁄…‰œflOM…œ£¨
°¢°≠‘⁄…‰œflOM…œ£¨![]() °¢
°¢![]() °¢
°¢![]() °≠æ˘Œ™µ»±fl»˝Ω«–Œ£¨»Ù
°≠æ˘Œ™µ»±fl»˝Ω«–Œ£¨»Ù![]() £¨‘Ú
£¨‘Ú![]() µƒ±fl≥§Œ™(°°°°)
µƒ±fl≥§Œ™(°°°°)
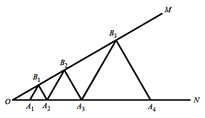
A.16B.64C.128D.256
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨“—÷™≈◊ŒÔœfl![]() ”Îx÷·¥”◊Û÷¡”“Ωª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„c£Æ
”Îx÷·¥”◊Û÷¡”“Ωª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„c£Æ

£®1£©»Ù≈◊ŒÔœflπ˝µ„T(1£¨-![]() )£¨«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
)£¨«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
£®2£©‘⁄µ⁄∂˛œÛœfiƒ⁄µƒ≈◊ŒÔœfl…œ «∑ҥʑ⁄µ„D£¨ πµ√“‘A°¢B°¢D»˝µ„Œ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜ABCœ‡À∆£ø»Ù¥Ê‘⁄£¨«Ûaµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
£®3£©»ÁÕº2£¨‘⁄(1)µƒÃıº˛œ¬£¨µ„Pµƒ◊¯±ÍŒ™(-1£¨1)£¨µ„Q(6£¨t) «≈◊ŒÔœfl…œµƒµ„£¨‘⁄x÷·…œ£¨¥”◊Û÷¡”“”–M°¢N¡Ωµ„£¨«“MN=2,Œ MN‘⁄x÷·…œ“∆∂صΩ∫Œ¥¶ ±£¨Àƒ±fl–ŒPQNMµƒ÷‹≥§◊Ó–°£ø«Î÷±Ω”–¥≥ˆ∑˚∫œÃıº˛µƒµ„Mµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£“™¥”–¬»Î—ßµƒ¡Ω√˚Ô˝Ãÿ≥§…˙¿Ó”¬°¢’≈∫∆÷–ÃÙ—°“ª»À≤Œº”–£º ï‘∂±»»¸£¨‘⁄ï‘∂◊®œÓ≤‚ ‘“‘º∞“‘∫Ûµƒ![]() ¥ŒÃ¯‘∂—°∞Œ»¸÷–£¨À˚√«µƒ≥…º®£®µ•Œª£∫
¥ŒÃ¯‘∂—°∞Œ»¸÷–£¨À˚√«µƒ≥…º®£®µ•Œª£∫![]() £©»Áœ¬±ÌÀ˘ æ£∫
£©»Áœ¬±ÌÀ˘ æ£∫
◊®œÓ≤‚ ‘∫Õ | ∆Ωæ˘ ˝ | ∑Ω≤Ó | |||||||
¿Ó”¬ |
|
|
|
|
|
|
|
| |
’≈∫∆ |
|
|
|
|
|
|
|
| |
![]() «Û’≈∫∆Õ¨—ß
«Û’≈∫∆Õ¨—ß![]() ¥Œ≤‚ ‘≥…º®µƒ∆Ωæ˘ ˝£¨¿Ó”¬Õ¨—ß
¥Œ≤‚ ‘≥…º®µƒ∆Ωæ˘ ˝£¨¿Ó”¬Õ¨—ß![]() ¥Œ≤‚ ‘≥…º®µƒ∑Ω≤Ó£ª
¥Œ≤‚ ‘≥…º®µƒ∑Ω≤Ó£ª
![]() «Îƒ„∑÷±¥”∆Ωæ˘ ˝∫Õ∑Ω≤ÓµƒΩ«∂»∑÷Œˆ¡Ω»À≥…º®µƒÃÿµ„£ª
«Îƒ„∑÷±¥”∆Ωæ˘ ˝∫Õ∑Ω≤ÓµƒΩ«∂»∑÷Œˆ¡Ω»À≥…º®µƒÃÿµ„£ª
![]() æ≠≤È‘ƒ¿˙Ωϱ»»¸µƒ◊ ¡œ£¨≥…º®»Ù¥ÔµΩ
æ≠≤È‘ƒ¿˙Ωϱ»»¸µƒ◊ ¡œ£¨≥…º®»Ù¥ÔµΩ![]() £¨æÕ∫‹ø…ƒ‹µ√µΩπ⁄渣¨ƒ„»œŒ™”¶—°À≠»•≤Œ»¸∂·π⁄渱»Ωœ”–∞—Œ’£øÀµ√˜¿Ì”…£ª
£¨æÕ∫‹ø…ƒ‹µ√µΩπ⁄渣¨ƒ„»œŒ™”¶—°À≠»•≤Œ»¸∂·π⁄渱»Ωœ”–∞—Œ’£øÀµ√˜¿Ì”…£ª
![]() “‘Õ˘µƒ∏√œÓ◊Ó∫√≥…º®µƒºÕ¬º «
“‘Õ˘µƒ∏√œÓ◊Ó∫√≥…º®µƒºÕ¬º «![]() £¨»Ù“™œÎ¥Ú∆∆ºÕ¬º£¨ƒ„»œŒ™”¶—°À≠»•≤Œ»¸£ø
£¨»Ù“™œÎ¥Ú∆∆ºÕ¬º£¨ƒ„»œŒ™”¶—°À≠»•≤Œ»¸£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨Ω´°˜ABO»∆µ„AÀ≥ ±’Ζ˝◊™µΩ°˜AB1C1µƒŒª÷√£¨µ„B°¢O∑÷±¬‰‘⁄µ„B1°¢C1¥¶£¨µ„B1‘⁄x÷·…œ£¨‘ŸΩ´°˜AB1C1»∆µ„B1À≥ ±’Ζ˝◊™µΩ°˜A1B1C2µƒŒª÷√£¨µ„C2‘⁄x÷·…œ£¨Ω´°˜A1B1C2»∆µ„C2À≥ ±’Ζ˝◊™µΩ°˜A2B2C2µƒŒª÷√£¨µ„A2‘⁄x÷·…œ£¨“¿¥ŒΩ¯––œ¬»•°≠£Æ»Ùµ„A£®![]() £¨0£©£¨B£®0£¨2£©£¨‘Úµ„B2018µƒ◊¯±ÍŒ™_____£Æ
£¨0£©£¨B£®0£¨2£©£¨‘Úµ„B2018µƒ◊¯±ÍŒ™_____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝ y1£Ωx£´2£¨y2£Ω4x£≠4£¨y3£Ω£≠![]() x£´1£¨»ÙŒfi¬€ x »°∫Œ÷µ£¨y ◊‹»° y1£¨y2£¨y3 ÷–µƒ◊Ó¥Û÷µ£¨‘Ú y µƒ◊Ó–°÷µ «__________£Æ
x£´1£¨»ÙŒfi¬€ x »°∫Œ÷µ£¨y ◊‹»° y1£¨y2£¨y3 ÷–µƒ◊Ó¥Û÷µ£¨‘Ú y µƒ◊Ó–°÷µ «__________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com