Question

【题目】【问题情境】一节数学课后，老师布置了一道课后练习题：

如图：已知在Rt△ABC中，AC=BC，∠ACB=90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1=∠2，FG⊥AB于点G，求证：△CDE≌△EGF．

（1）阅读理解，完成解答

本题证明的思路可用下列框图表示：

根据上述思路，请你完整地书写这道练习题的证明过程；

（2）特殊位置，证明结论

若CE平分∠ACD，其余条件不变，求证：AE=BF；

（3）知识迁移，探究发现

如图，已知在Rt△ABC中，AC=BC，∠ACB=90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC=EF，请直接写出AE与BF的数量关系．（不必写解答过程）

Answer 1

【答案】(1)证明过程见解析；(2)证明过程见解析；(3)AE=BF.

【解析】

试题分析：(1)先证明CE=EF，根据AAS即可证明△CDE≌△EGF；(2)先证∠ACE=∠2，再证明△ACE≌△BEF，即可得出AE=BF；(3)作EH⊥BC与H，设DE=x，求出AE=3x，再证出BF=x，即可得出结论．

试题解析：(1)∵AC=BC，∠ACB=90°， ∴∠A=∠B=45°， ∵CD⊥AB， ∴∠CDB=90°，

∴∠DCB=45°， ∵∠ECF=∠DCB+∠1=45°+∠1，∠EFC=∠B+∠2=45°+∠2，∠1=∠2， ∴∠ECF=∠EFC，

∴CE=EF， ∵CD⊥AB，FG⊥AB， ∴∠CDE=∠EGF=90°，

在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；

(2)由(1)得：CE=EF，∠A=∠B， ∵CE平分∠ACD， ∴∠ACE=∠1， ∵∠1=∠2，∴∠ACE=∠2，

在△ACE和△BEF中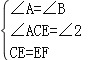，，∴△ACE≌△BEF（AAS），∴AE=BF；

(3)AE=BF，作EH⊥BC与H，如图3所示：

设DE=x，根据题意得：BE=DE=x，AD=BD=2x，CD=AD=2x，AE=3x， 根据勾股定理得：BC=AC=2x，

∵∠ABC=45°，EH⊥BC， ∴BH=x， ∴CH=BC﹣BH=x， ∵EC=EF， ∴FH=CH=x，

∴BF=x﹣x=x， ∴， ∴AE=BF．