
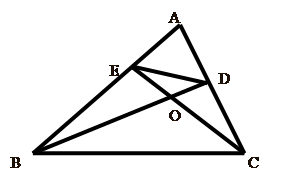
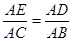 ;
; 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:不详 题型:解答题
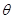 (0°<
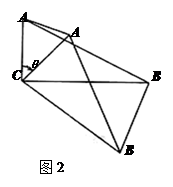
(0°<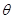 <180°),得到△A′B′C.
<180°),得到△A′B′C.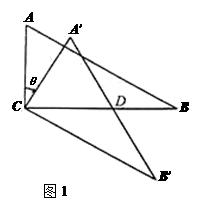
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ∽ △QWP;
∽ △QWP;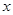 为何值时,△PQW为直角三角形?
为何值时,△PQW为直角三角形? 
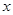 为____▲_____时,线段MN最短?
为____▲_____时,线段MN最短?
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
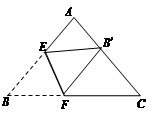
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

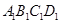 的面积是多少平方米?
的面积是多少平方米?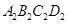 做一个纸箱比方案1更优,你认为呢?请说明理由.
做一个纸箱比方案1更优,你认为呢?请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com