
【题目】如图,函数![]() 与
与![]() 的图象交于
的图象交于![]() .
.
(1)求出m、n的值;
(2)直接写出不等式![]() 的解集;
的解集;
(3)求出![]() 的面积.
的面积.

【答案】(1)m=-0.75,n=2.5;(2)x>2.5;(3)S△ABP=![]()
【解析】
(1)根据凡是函数图象经过的点必能满足解析式把P点坐标代入y=-2x+3可得n的值,进而可得P点坐标,再把P点坐标代入y=-![]() x+m可得m的值;
x+m可得m的值;
(2)根据函数图象可直接得到答案;
(3)首先求出A、B两点坐标,进而可得△ABP的面积
解:(1)∵y=-2x+3过P(n,-2).
∴-2=-2n+3,解得:n=![]() ,
,
∴P(![]() ,-2),
,-2),
∵y=![]() x+m的图象过P(
x+m的图象过P(![]() ,-2).
,-2).
∴-2=![]() ×
×![]() +m,
+m,
解得:m=![]() ;
;
(2)根据图像可知,x>![]() 时,y=-
时,y=-![]() x
x![]() 的图像在y=-2x+3的上方,
的图像在y=-2x+3的上方,
∴不等式![]() 的解集为:x>
的解集为:x>![]() ;
;
(3)∵当y=-2x+3中,x=0时,y=3,
∴A(0,3),
∵![]() 中,x=0时,y=-
中,x=0时,y=-![]() ,
,
∴B(0,-![]() ),
),
∴AB=![]() ;
;
∴△ABP的面积:![]() .
.


科目:初中数学 来源: 题型:
【题目】为了解本校九年级学生期末数学考试情况,在九年级随机抽取了一部分学生 的期末数学成绩为样本,分为 A(90~100 分);B(80~89 分);C(60~79 分);D(0~59 分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下 问题.
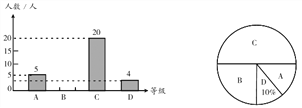
(1)这次随机抽取的学生共有多少人?
(2)请补全条形统计图;
(3)这个学校九年级共有学生 1200 人,若分数为 80 分(含 80 分)以上为优秀,请估 计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应“弘扬传统文化”的号召,某学校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.

大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)求活动启动之初学生“一周诗词诵背数量”的中位数;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数;
(3)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).
设这种双肩包每天的销售利润为w元.
(1)求w与x之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
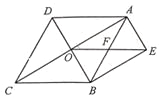
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=10,AC=16,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=x+n﹣2与直线l2:y=mx+n相交于点P(1,2).
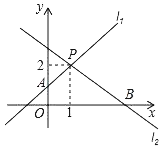
(1)求m,n的值;
(2)请结合图象直接写出不等式mx+n>x+n﹣2的解集.
(3)若直线l1与y轴交于点A,直线l2与x轴交于点B,求四边形PAOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,在等边三角形ABC内有一点P,且PA=2,PB=![]() ,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1、求∠BPC度数的大小和等边三角形ABC的边长.
李明同学的思路是:将△BPC绕点B逆时针旋转60°,画出旋转后的图形(如图2),连接PP′,可得△P′PC是等边三角形,而△PP′A又是直角三角形(由勾股定理的逆定理可证),从而得到∠BPC=∠AP′B=__________;,进而求出等边△ABC的边长为__________;
问题得到解决.
请你参考李明同学的思路,探究并解决下列问题:如图3,在正方形ABCD内有一点P,且PA=![]() ,BP=
,BP=![]() ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在课外学习时遇到这样一个问题:
定义:如果二次函数y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常数)与y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常数)满足a1+a2=0,b1=b2,c1+c2=0,则称这两个函数互为“旋转函数”.
求函数y=﹣x2+4x﹣3的“旋转函数”.小明是这样思考的:由函数y=﹣x2+4x﹣3可知,a1=﹣1,b1=4,c1=﹣3,根据a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能确定这个函数的“旋转函数”.
(1)请参考小明的方法写出函数y=﹣x2+4x﹣3的“旋转函数”;
(2)若函数![]() 与y=x2﹣3nx+n互为“旋转函数”,求
与y=x2﹣3nx+n互为“旋转函数”,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com