
【题目】若存在3个互不相同的有理数a,b,c,使得|1﹣a|+|1﹣3a|+|1﹣4a|=|1﹣b|+|1﹣3b|+|1﹣4b|=|1﹣c|+|1﹣3c|+|1﹣4c|=t,则t=
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)请问一元二次方程x2﹣3x+2=0是倍根方程吗?如果是,请说明理由.
(2)若一元二次方程ax2+bx﹣6=0是倍根方程,且方程有一个根为2,求a、b的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
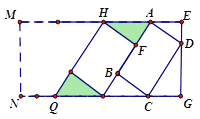
【题目】如图,在一个矩形停车场MNGE中,矩形ABCD是一辆机动车停放的车位示意图,经测量得AB=5.4米,BC=2.4米,AF=1.8米,HF⊥AB.其中HF是另一车位的一边,所有车位尺寸一样,并按图示并列划定.
(1)求路宽EG;
(2)若停车场的长EM=85米,求这个停车场的停车车位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=
的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC=![]() .
.
(1)求该反比例函数和一次函数的解析式.
(2)求△BOC的面积.
(3)P是x轴上的点,且△PAC的面积与△BOC的面积相等,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+2与x轴、y轴分别交于点A、B,点C(1,a)是该直线与双曲线y=![]() 的一个交点,过点C作CD垂直y轴,垂足为D,且S△BCD=1.
的一个交点,过点C作CD垂直y轴,垂足为D,且S△BCD=1.
(1)求双曲线的解析式.
(2)设直线与双曲线的另一个交点为E,求点E的坐标.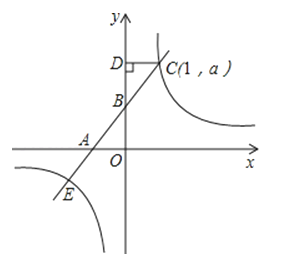
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半.电视机与洗衣机的进价和售价如下表:
类 别 | 电视机 | 洗衣机 |
进价(元/台) | 1 800 | 1 500 |
售价(元/台) | 2 000 | 1 600 |
计划购进电视机和洗衣机共 100 台,商店最多可筹集资金161 800 元.
(1)请你帮助商店算一算有多少种进货方案(不考虑除进价之外的其他费用);
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最大的利润(利润=售价-进价).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com