
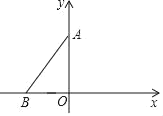
【题目】如图,在平面直角坐标系中,点A(0,4)、B(﹣3,0),将线段AB沿x轴正方向平移n个单位得到菱形ABCD.
(1)画出菱形ABCD,并直接写出n的值及点D的坐标;
(2)已知反比例函数y=![]() 的图象经过点D,ABMN的顶点M在y轴上,N在y=
的图象经过点D,ABMN的顶点M在y轴上,N在y=![]() 的图象上,求点M的坐标;
的图象上,求点M的坐标;
(3)若点A、C、D到某直线l的距离都相等,直接写出满足条件的直线解析式.
【答案】(1)n=5,点D坐标为(5,4);(2)M(0,![]() );(3)y=﹣2x+9.
);(3)y=﹣2x+9.
【解析】
(1)由勾股定理和菱形的性质可得AB=BC=CD=AD=5,即可求n的值及点D的坐标;
(2)过点N作NH⊥OA于点H,由平行四边形的性质可得AN=BM,AN∥BM,可得∠BMO=∠NAH,由“AAS”可证△ANH≌△MBO,可得HN=BO=3,MO=AH,即可求点M坐标;
(3)由点A、C、D到某直线l的距离都相等,可得直线l是△ACD的中位线所在直线,由待定系数法可求直线解析式.
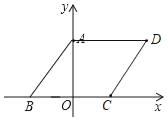
解:(1)如图,
∵点A(0,4)、B(﹣3,0),
∴AO=4,BO=3,
∴AB=![]() =5,
=5,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∵将线段AB沿x轴正方向平移n个单位得到菱形ABCD,
∴n=5,点C坐标为(2,0),点D坐标为(5,4);
(2)∵反比例函数y=![]() 的图象经过点D,
的图象经过点D,
∴k=4×5=20,
∵N在y=![]() 的图象上,
的图象上,
∴设点N(a,![]() ),
),
如图,过点N作NH⊥OA于点H,
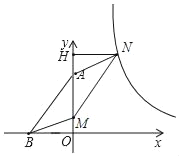
∵四边形ABMN是平行四边形
∴AN=BM,AN∥BM,
∴∠BMA=∠NAM,
∴∠BMO=∠NAH,且AN=BM,∠BOM=∠NHA=90°,
∴△ANH≌△MBO(AAS),
∴HN=BO=3,MO=AH,
∴HN=a=3,HO=![]() ,
,
∴OM=AH=HO﹣AO=![]() ,
,
∴点M(0,![]() );
);
(3)∵点A、C、D到某直线l的距离都相等,
∴直线l是△ACD的中位线所在直线,
如图所示:
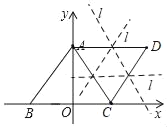
若直线l过线段AC,CD中点,
∴直线l的解析式为:y=2,
若直线l过线段AD,AC中点,即直线l过点(![]() ,4),点(1,2),
,4),点(1,2),
设直线l的解析式为:y=mx+n
∴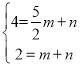 ,
,
解得:m=![]() ,n=
,n=![]() ,
,
∴直线l的解析式为:y=![]() ,
,
若直线l过线段AD,CD中点,即直线l过点(![]() ,4),点(
,4),点(![]() ,2),
,2),
设直线l解析式为:y=kx+b
∴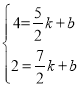 ,
,
解得:k=﹣2,b=9,
∴直线l的解析式为:y=﹣2x+9.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,抛物线与直线
,抛物线与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形?若存在,请直接写出点
为底边的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)![]() 点在
点在![]() 轴上且位于点
轴上且位于点![]() 的左侧,若以
的左侧,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的有( )个
①绝对值相等的两数相等.②若a,b互为相反数,则![]() =﹣1.③如果a大于b,那么a的倒数小于b的倒数.④任意有理数都可以用数轴上的点来表示.⑤x2﹣2x﹣33x3+25是五次四项.⑥两个负数比较大小,绝对值大的反而小.⑦一个数的相反数一定小于或等于这个数.⑧正数的任何次幂都是正数,负数的任何次幂都是负数.
=﹣1.③如果a大于b,那么a的倒数小于b的倒数.④任意有理数都可以用数轴上的点来表示.⑤x2﹣2x﹣33x3+25是五次四项.⑥两个负数比较大小,绝对值大的反而小.⑦一个数的相反数一定小于或等于这个数.⑧正数的任何次幂都是正数,负数的任何次幂都是负数.
A. 4个 B. 5个 C. 6个 D. 7个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=![]() ﹣6x+4的顶点A在直线y=kx﹣2上.
﹣6x+4的顶点A在直线y=kx﹣2上.
(1)求直线的函数表达式;
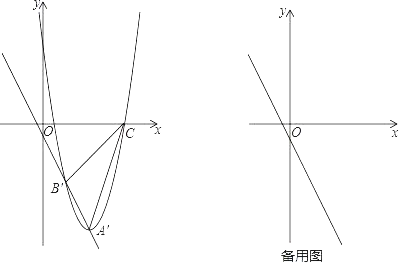
(2)现将抛物线沿该直线方向进行平移,平移后的抛物线的顶点为A′,与直线的另一交点为B′,与x轴的右交点为C(点C不与点A′重合),连接B′C、A′C.
ⅰ)如图,在平移过程中,当点B′在第四象限且△A′B′C的面积为60时,求平移的距离AA′的长;
ⅱ)在平移过程中,当△A′B′C是以A′B′为一条直角边的直角三角形时,求出所有满足条件的点A′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是张亮、李娜两位同学零花钱全学期各项支出的统计图.根据统计图,下列对两位同学购买书籍支出占全学期总支出的百分比作出的判断中,正确的是( )


A. 张亮的百分比比李娜的百分比大 B. 张娜的百分比比张亮的百分比大
C. 张亮的百分比与李娜的百分比一样大 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
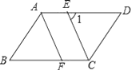
【题目】如图,在ABCD中,CE平分∠BCD,且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠B=52°,求∠1的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,每个小正方形的边长都为1,![]() 和
和![]() 的顶点都在格点上,回答下列问题:
的顶点都在格点上,回答下列问题:
![]() 可以看作是
可以看作是![]() 经过若干次图形的变化
经过若干次图形的变化![]() 平移、轴对称、旋转
平移、轴对称、旋转![]() 得到的,写出一种由
得到的,写出一种由![]() 得到
得到![]() 的过程:______;
的过程:______;
![]() 画出
画出![]() 绕点B逆时针旋转
绕点B逆时针旋转![]() 的图形
的图形![]() ;
;
![]() 在
在![]() 中,点C所形成的路径的长度为______.
中,点C所形成的路径的长度为______.
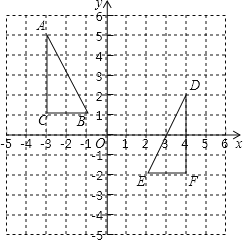
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
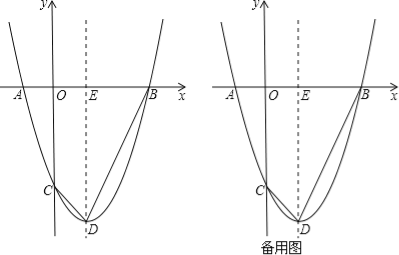
(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com