14.阅读理解:给定次序的n个数a1,a2,…,an,记Sk=a1+a2+…ak,为前k个数的和(1≤k≤n),定义A=(S1+S2+…+Sn)÷n称它们的“凯森和”,如a1=2,a2=3,a3=3,则s1=2,s2=5,s3=8,凯森和A=(2+5+8)÷3=5,若有99个数a1,a2,…,a99的“凯森和”为100,则添上21后的100个数21,a1,a2,…,a99的凯森和为120.
分析 首先求出s1+s2+s3+…+s99的值,然后再求添上21后的100个数21,a1,a2,…,a99的凯森和.
解答 解:∵99个数a1,a2,…,a99的“凯森和”为100,
∴(S1+S2+…+S99)÷99=100,
∴S1+S2+…+S99=9900,
(21+S1+21+S2+21+…+S99+21)÷100
=(21×100+S1+S2+…+S99)÷100
=(21×100+9900)÷100
=21+99
=120.
故答案为:120.
点评 本题考查了新定义运算,正确理解凯森和的含义是解答本题的关键.

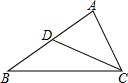 如图,D是AB上的一点.△ABC∽△ACD,且AD=2,BD=4,∠ADC=65°,∠B=43°,则∠A=72°,AC=2$\sqrt{3}$.
如图,D是AB上的一点.△ABC∽△ACD,且AD=2,BD=4,∠ADC=65°,∠B=43°,则∠A=72°,AC=2$\sqrt{3}$.