
 如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A(m,2).
如图,直线y=2x与双曲线y=$\frac{k}{x}$交于点A(m,2).分析 (1)把A(m,2)代入直线y=2x求出m=1,得出A(1,2),即可得出结果;
(2)作AM⊥x轴于M,PN⊥x轴于N,设P(a,b),则ab=2①,由梯形AMNP的面积得出$\frac{1}{2}$(2+b)(a-1)=2①,由①②求出a和b的值,得出P(1+$\sqrt{2}$,2$\sqrt{2}$-2),设直线PB的解析式为y=2x+b,把点P坐标代入求出b=-4即可.
解答 解:(1)把A(m,2)代入直线y=2x得:m=1,
∴A(1,2),
∴k=1×2=2;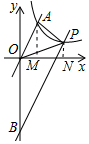
(2)作AM⊥x轴于M,PN⊥x轴于N,如图所示:
设P(a,b),则ab=2,
∵双曲线y=$\frac{2}{x}$,
∴△AOM的面积=△PON的面积=$\frac{1}{2}$×2=1,
∵△AOP的面积为2,
∴梯形AMNP的面积=2,即$\frac{1}{2}$(2+b)(a-1)=2①,
由①②得:$\left\{\begin{array}{l}{a=1+\sqrt{2}}\\{b=2\sqrt{2}-2}\end{array}\right.$或$\left\{\begin{array}{l}{a=1-\sqrt{2}}\\{b=-2\sqrt{2}-2}\end{array}\right.$(舍去),
∴P(1+$\sqrt{2}$,2$\sqrt{2}$-2),
∵直线PB与直线y=2x平行,
∴设直线PB的解析式为y=2x+b,
把点P坐标代入得:2+2$\sqrt{2}$+b=2$\sqrt{2}$-2,
解得:b=-4,
∴直线PB的解析式为y=2x-4.
点评 此题主要考查了反比例函数与一次函数的交点,两条直线的平行关系、坐标与图形性质;求出点P的坐标是解决问题(2)的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{49}$=-7 | B. | $\sqrt{49}$=±7 | C. | -$\sqrt{49}$=±7 | D. | ±$\sqrt{49}$=7 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省七年级3月月考数学试卷(解析版) 题型:单选题
已知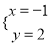 是二元一次方程组
是二元一次方程组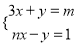 的
的 解,则m-n的值是( )
解,则m-n的值是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省盐城市盐都区西片七年级下学期第一次月考数学试卷(解析版) 题型:填空题
若△ABC中,∠A:∠B:∠C=2:3:4,则△ABC是 三角形.(填:锐角或直角或钝角)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com