
【题目】如图,△ABC中,∠ABC=90°,F是AC的中点,过AC上一点D作DE//AB,交BF的延长线于点E,AG⊥BE,垂足是G,连接BD、AE.
(1)求证:△ABC∽△BGA;
(2)若AF=5,AB=8,求FG的长;
(3)当AB=BC,∠DBC=30°时,求 ![]() 的值.
的值.
【答案】
(1)
证明:∵∠ABC=90°,F是AC的中点,
∴BF= ![]() AC=AF,
AC=AF,
∴∠FAB=∠FBA,
∵AG⊥BE,
∴∠AGB=90°,
∴∠ABC=∠AGB,
∴△ABC∽△BGA;
(2)
∵AF=5,
∴AC=2AF=10,BF=5,
∵△ABC∽△BGA,
∴ ![]() ,
,
∴BG= ![]() =
= ![]() =
= ![]() ,
,
∴FG=BG﹣BF= ![]() ﹣5=
﹣5= ![]()
(3)
延长ED交BC于H,如图所示:
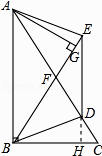
则DH⊥BC,
∴∠DHC=90°,
∵AB=AC,F为AC的中点,
∴∠C=45°,∠CBF=45°,
∴△DHC、△BEH是等腰直角三角形,
∴DH=HC,EH=BH,
设DH=HC=a,
∵∠DBC=30°,
∴BD=2a,BH= ![]() a,
a,
∴EH= ![]() a,
a,
∴DE=( ![]() ﹣1)a,
﹣1)a,
∴ ![]() =
= ![]() .
.
【解析】(1)由直角三角形斜边上的中线性质得出BF=AF,得出∠FAB=∠FBA,再由∠ABC=∠AGB=90°,即可证出△ABC∽△BGA;(2)先求出AC、BF,再由三角形相似得出比例式 ![]() ,求出BG,即可得出FG;(3)延长ED交BC于H,则DH⊥BC,先证出△DHC、△BEH是等腰直角三角形,得出DH=HC,EH=BH,设DH=HC=a,求出BD=2a,BH=
,求出BG,即可得出FG;(3)延长ED交BC于H,则DH⊥BC,先证出△DHC、△BEH是等腰直角三角形,得出DH=HC,EH=BH,设DH=HC=a,求出BD=2a,BH= ![]() a,得出EH、DE,即可求出
a,得出EH、DE,即可求出 ![]() 的值.
的值.
【考点精析】利用相似三角形的应用对题目进行判断即可得到答案,需要熟知测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.


科目:初中数学 来源: 题型:
【题目】如图在数轴上A点表示数![]() ,B点表示数
,B点表示数![]() ,且
,且![]() 、
、![]() 满足
满足![]() ,
,
![]()
(1)点A表示的数为_______;点B表示的数为__________;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=3BC,则C点表示的数__________;
(3)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请分别表示出甲、乙两小球到原点的距离(用含t的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
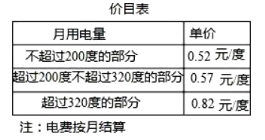
(1)若某户居民10月份电费78元,则该户居民10月份用电________度;
(2)若该户居民2月份用电340度,则应缴电费________元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数y= ![]() (k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE .
(k≠0,且k为常数)的图象过点E,且S△AOE=3S△OBE . 
(1)求k的值;
(2)反比例函数图象与线段BC交于点D,直线y= ![]() x+b过点D与线段AB交于点F,延长OF交反比例函数y=
x+b过点D与线段AB交于点F,延长OF交反比例函数y= ![]() (x<0)的图象于点N,求N点坐标.
(x<0)的图象于点N,求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;
(2)模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;
(3)拓展应用:某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A,B,C,表示的数分别是﹣4,﹣2,3.
![]()
(1)若使C、B两点的距离是A、B两点的距离的2倍,则需将点C向左移动 个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒a个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒:
①点A、B、C表示的数分别是 、 、 (用含a、t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当a为何值时,5d1﹣3d2的值不会随着时间t的变化而改变,并求此时5d1﹣3d2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】取一张矩形的纸片进行折叠,具体操作过程如下: 第一步:先把矩形ABCD对折,折痕为MN,如图(1);
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B′,得Rt△AB′E,如图(2);
第三步:沿EB′线折叠得折痕EF,如图(3).
若AB= ![]() ,则EF的值是( )
,则EF的值是( )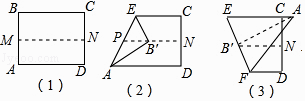
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4),延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1…按这样的规律进行下去,第2018个正方形的面积为( )

A. 20×(![]() )2017 B. 20×(
)2017 B. 20×(![]() )2018 C. 20×(
)2018 C. 20×(![]() )4036 D. 20×(
)4036 D. 20×(![]() )4034
)4034
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com