
【题目】已知关于x的一元二次方程x2﹣3x+k=0方程有两实根x1和x2.
(1)求实数k的取值范围;
(2)当x1和x2是一个矩形两邻边的长且矩形的对角线长为![]() ,求k的值.
,求k的值.
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知:y=y1﹣y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时y=1.
(1)求y关于x的函数关系式.
(2)求x=﹣![]() 时,y的值.
时,y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
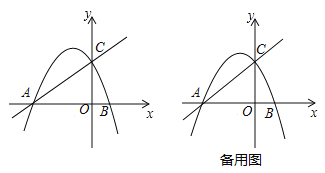
【题目】在直角坐标平面内,直线y=![]() x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣![]() +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为![]() 的矩形纸板
的矩形纸板![]() ,如图
,如图![]() ,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面
,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面![]() 为矩形,如图
为矩形,如图![]() ,设小正方形的边长为
,设小正方形的边长为![]() 厘米.、
厘米.、
(1)若矩形纸板的一个边长为![]() .
.
①当纸盒的底面积为![]() 时,求
时,求![]() 的值;
的值;
②求纸盒的侧面积的最大值;
(2)当![]() ,且侧面积与底面积之比为
,且侧面积与底面积之比为![]() 时,求
时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,P是CD上一点,且AP和BP分别平分∠DAB和∠CBA.
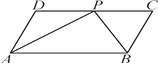
(1)求∠APB的度数;
(2)如果AD=5 cm,AP=8 cm,求△APB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求画图
(1)如图,平面上有五个点A,B,C,D,E. 按下列要求画出图形.
①连接BD;
②画直线AC交BD于点M;
③过点A作线段AP⊥BD于点P;
④请在直线AC上确定一点N,使B,E两点到点N的距离之和最小(保留作图痕迹).
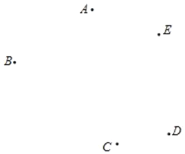
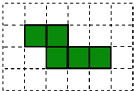
(2)小强用5个大小一样的正方形制成如图所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.注意:只需添加一个符合要求的正方形,并用阴影表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明上周零花钱使用情况:(规定:超过50元记为正,少于50元记为负)
星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
+11 | +10 | ﹣17 | +18 | ﹣12 |
请你解答以下问题:
(1)上星期五小明用了多少零花钱;
(2)上星期四比上星期三多花了多少零花钱;
(3)求上周平均每天用多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦放假时,小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥.早上从家里出发,向东走了5千米到超市买东西,然后又向东走了2.5千米到爷爷家,下午从爷爷家出发向西走了10千米到姥爷家,晚上返回家里.
(1)若以小明家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来;
![]()
(2)超市和姥爷家相距多少千米?
(3)若小轿车每千米耗油0.08升,求小明一家从出发到返回家,小轿车的耗油量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com