
本题10分)
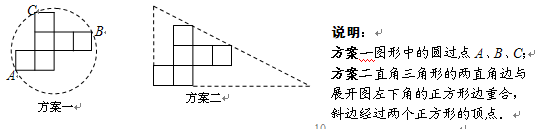
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:

纸片利用率=×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2013届江苏省大丰市第四中学九年级12月月考数学试卷(带解析) 题型:解答题
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格图中进行下列操作:
(1) 利用网格确定该圆弧所在圆的圆心D点的位置,则D点坐标为 ;
(2) 连接AD、CD,则⊙D的半径为 (结果保留根号),∠ADC的度数为 ;
(3) 若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).(本题10分) 
查看答案和解析>>
科目:初中数学 来源:2012届浙江省金衢十一校联考校联考九年级第一次考试数学卷 题型:解答题
本题10分)
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计: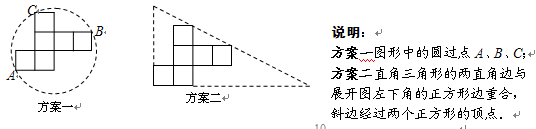
纸片利用率=×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省金衢十一校联考校联考九年级第一次考试数学卷 题型:解答题
本题10分)
操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:
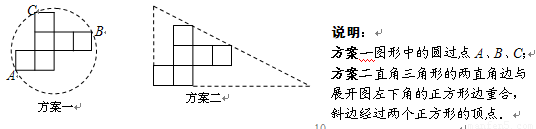
纸片利用率=×100%
发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.请帮忙计算方案二的利用率,并写出求解过程.
探究:(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com