
【题目】细观察,找规律
下列各图中的MA1与NAn平行.

(1)图①中的∠A1+∠A2= ______ 度,
图②中的∠A1+∠A2+∠A3= ______ 度,
图③中的∠A1+∠A2+∠A3+∠A4= ______ 度,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5= ______ 度,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11= ______ 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An+1= ______
(3)请你证明图②的结论.
【答案】180, 360, 540, 720, 1800; (2)180n度;(3)见解析.
【解析】
(1)首先过各点作MA1的平行线,由MA1∥NA2,可得各线平行,根据两直线平行,同旁内角互补,即可得到结论;
(2)根据(1)中的规律,即可得到第n个图中的∠A1+∠A2+∠A3+…+∠An+1的度数;
(3)先过A2作A2B∥A1M,根据A2B∥A1M∥A3N,可得∠A1+∠1=180°,∠A3+∠2=180°,进而得出∠A1+∠A1A2A3+∠A3=360°.
解:(1)
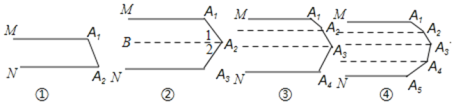
根据平行线的性质,可得图①中的∠A1+∠A2=180度,
根据平行线的性质,可得图②中的∠A1+∠A2+∠A3=360度,
根据平行线的性质,可得图③中的∠A1+∠A2+∠A3+∠A4=540度,
根据平行线的性质,可得图④中的∠A1+∠A2+∠A3+∠A4+∠A5=720度;
…,
根据平行线的性质,可得第⑩个图中的∠A1+∠A2+∠A3+…+∠A11= 1800 度
(2)根据平行线的性质,可得第n个图中的∠A1+∠A2+∠A3+…+∠An+1=180n度;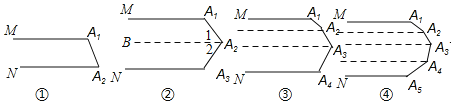
(3)如图②,过A2作A2B∥A1M,
∵MA1与N A3平行,
∴A2B∥A1M∥A3N,
∴∠A1+∠1=180°,∠A3+∠2=180°,
又∵∠1+∠2=∠A1A2A3,
∴∠A1+∠A1A2A3+∠A3=180°+180°=360°.
故答案为:(1)180,360,540,720,1800;(2)180n度;(3)见解析.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠A=∠D=72°,∠ACB=∠DBC=36°,则图中等腰三角形的个数是( )
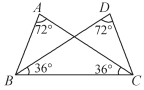
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC. (1)若∠A=36,在△ABC中画一条线段,能得到2个等腰三角形(不包括△ABC),这2个等腰三角形的顶角的度数分别是_____;(2)若∠A≠36, 当∠A=_____时,在等腰△ABC中画一条线段,能得到2个等腰三角形(不包括△ABC).(写出两个答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为表彰在美术展览活动中获奖的同学,老师决定购买一些水笔和颜料盒作为奖品,请你根据图中所给的信息,解答下列问题; 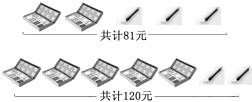
(1)求出每个颜料盒,每支水笔各多少元?
(2)若学校计划购买颜料盒和水笔共20个,所用费用不超过340元,则颜料盒至多购买多少个?
(3)恰逢商店举行优惠促销活动,具体办法如下:颜料盒按七折优惠,水笔10支以上超出部分按八折优惠,若学校决定购买同种数量的同一奖品,并且该奖品的数量超过10件,请你帮助分析,购买颜料盒合算还是购买水笔合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
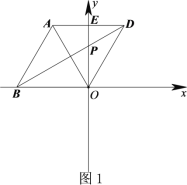
【题目】在平面直角坐标系xOy中,△![]() 为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
(1)如图1,若点B在x轴的负半轴上时,直接写出![]() 的度数;
的度数;
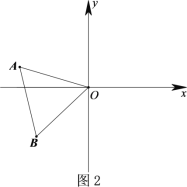
(2)如图2,将△![]() 绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为
绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为![]() ,60<
,60<![]() <90,依题意补全图形,并求出
<90,依题意补全图形,并求出![]() 的度数;(用含
的度数;(用含![]() 的式子表示)
的式子表示)
(3)在第(2)问的条件下,用等式表示线段BP,PE,PO之间的数量关系.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你会求(a﹣1)(a2012+a2011+a2010+…+a2+a+1)的值吗?这个问题看上去很复杂,我们可以先考虑简单的情况,通过计算,探索规律:
![]() ,
,
![]() ,
,
![]() ,
,
(1)由上面的规律我们可以大胆猜想,得到(a﹣1)(a2014+a2013+a2012+…+a2+a+1)=
利用上面的结论,求:
(2)22014+22013+22012+…+22+2+1的值是 .
(3)求52014+52013+52012+…+52+5+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
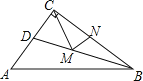
【题目】如图,△ABC中,∠ACB=90°,AC =3,BC =4,AB=5,BD平分∠ABC,如果M、N分别为BD、BC上的动点,那么CM+MN的最小值是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com