
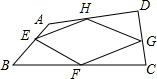
 我们把依次连结任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,依次连结各边中点得到的中点四边形EFGH.
我们把依次连结任意一个四边形各边中点得到的四边形叫做中点四边形.如图,在四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,依次连结各边中点得到的中点四边形EFGH.分析 (1)根据四边形的形状,及三角形中位线的性质可判断出四边形EFGH是平行四边形;
(2)连接AC、利用三角形的中位线定理可得出HG=EF、EF∥GH,继而可判断出四边形EFGH的形状;
(3)根据中位线的与对角线平行的性质,因此顺次连接四边中点可以得到一个相邻的边互相垂直的四边形,根据矩形的定义,邻边垂直的四边形为矩形,同理可得矩形的中点四边形形状.
解答  (1)解:中点四边形EFGH的形状是平行四边形.
(1)解:中点四边形EFGH的形状是平行四边形.
故答案为:平行四边形;
(2)证明:如图1,连接AC,
∵E是AB的中点,F是BC的中点,
∴EF∥AC,EF=$\frac{1}{2}$AC,
同理HG∥AC,HG=$\frac{1}{2}$AC,
综上可得:EF∥HG,EF=HG,
故四边形EFGH是平行四边形.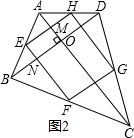
(3)解:对角线互相垂直的四边形,它的中点四边形是:矩形;矩形的中点四边形是菱形.
理由:如图2,∵E、F、G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD,
∴四边形EFGH是平行四边形,
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形,
∴∠MEN=90°,
∴四边形EFGH是矩形.
故答案为:矩形,菱形.
点评 此题考查了三角形的中位线定理及平行四边形的判定、矩形、菱形的判定等知识,正确掌握特殊四边形的判定方法是解题关键.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
 如图是由两个长方体组成的几何体,这两个长方体的底面都是正方形,按要求完成下列各小题.
如图是由两个长方体组成的几何体,这两个长方体的底面都是正方形,按要求完成下列各小题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
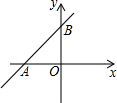 如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点.
如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?
如图所示,有一个圆柱,它的高为9厘米,底面周长为24厘米,在圆柱下底面的A点有一只蚂蚁要沿侧面到上底面B点取食物,问它爬行的最短路程是多少厘米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
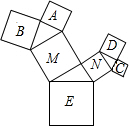 如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是3,5,2,3,则最大的正方形E的面积为多少?
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是3,5,2,3,则最大的正方形E的面积为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com