
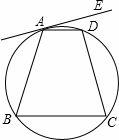
如图所示的直线AE与四边形ABCD的外接圆相切于A点.若∠DAE=12°,![]() 、
、![]() 、
、![]() 三弧的度数相等,则∠ABC的度数为何?( )
三弧的度数相等,则∠ABC的度数为何?( )
|
| A. | 64 | B. | 65 | C. | 67 | D. | 68 |
考点:
切线的性质。
专题:
计算题。
分析:
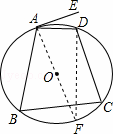
作直径AF,连接DF,根据切线的性质求出∠F的度数,求出弧AD的度数,求出DC的度数,得出弧ADC的度数,即可求出答案.
解答:
解:作直径AF,连接DF,
∵AE是⊙O的切线,
∴∠EAF=90°,
∵∠ADF=90°,
∴∠EAD+∠DAF=90°,∠F+∠DAF=90°,
∴∠F=∠DAE
∵∠DAE=12°(已知),
∴∠F=12°,
∴弧AD的度数是2×12°=24°,
∴![]() 、
、![]() 、
、![]() 三弧的度数相等,
三弧的度数相等,
∴弧CD的度数是![]() ×(360°﹣24°)=112°,
×(360°﹣24°)=112°,
∴弧ADC的度数是24°+112°=136°,
∴∠ABC=![]() ×136°=68°,
×136°=68°,
故选D.
点评:
本题考查了切线的性质的应用,能求出弧AD的度数是解此题的关键,弦切角等于该弦所夹弧所对的圆周角,主要培养学生运用性质进行推理和计算的能力.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
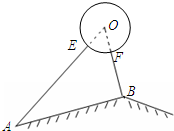 安装在屋顶的太阳能热水器的横截面示意图如图所示.集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O处,⊙O的半径为0.2m,AO与屋面AB的夹角为32°,BF⊥AB于B,AB=2m,求支架BF的长(精确到0.1m).参考数据:sin32°=0.32,cos32°=0.84,tan32°=0.62.
安装在屋顶的太阳能热水器的横截面示意图如图所示.集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O处,⊙O的半径为0.2m,AO与屋面AB的夹角为32°,BF⊥AB于B,AB=2m,求支架BF的长(精确到0.1m).参考数据:sin32°=0.32,cos32°=0.84,tan32°=0.62.查看答案和解析>>
科目:初中数学 来源: 题型:
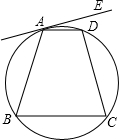 (2012•台湾)如图所示的直线AE与四边形ABCD的外接圆相切于A点.若∠DAE=12°,
(2012•台湾)如图所示的直线AE与四边形ABCD的外接圆相切于A点.若∠DAE=12°, |
| AB |
 |
| BC |
 |
| CD |
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
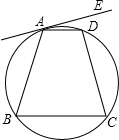 如图所示的直线AE与四边形ABCD的外接圆相切于A点.若∠DAE=12°,
如图所示的直线AE与四边形ABCD的外接圆相切于A点.若∠DAE=12°, 、
、 、
、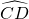 三弧的度数相等,则∠ABC的度数为何?
三弧的度数相等,则∠ABC的度数为何?查看答案和解析>>
科目:初中数学 来源:2012年台湾省中考数学试卷(解析版) 题型:选择题
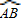 、
、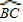 、
、 三弧的度数相等,则∠ABC的度数为何?( )
三弧的度数相等,则∠ABC的度数为何?( )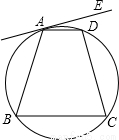
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com