
 ��ͼ����ƽ��ֱ������ϵ�У���x�����ڵ�ֱ������ԭ��O����ʱ�뷽����ת���ǶȺ�����ֱ���뺯��y=$\frac{\sqrt{3}}{x}$��ͼ��ֱ��ڵ�B��D����֪��A��-m��0����C��m��0����m��0��
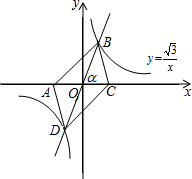
��ͼ����ƽ��ֱ������ϵ�У���x�����ڵ�ֱ������ԭ��O����ʱ�뷽����ת���ǶȺ�����ֱ���뺯��y=$\frac{\sqrt{3}}{x}$��ͼ��ֱ��ڵ�B��D����֪��A��-m��0����C��m��0����m��0������ ��1�����ڷ�����������ͼ����һ�����ĶԳ�ͼ�Σ���B��D�������������뷴��������ͼ��Ľ��㣬���Ե�B���D���ڵ�O�����ĶԳƣ���OB=OD����OA=OC�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ��ɵó��ı���ABCD����״��
��2���ѵ�B��p��$\sqrt{3}$������y=$\frac{\sqrt{3}}{x}$�������p��ֵ����B��BE��x����E����Rt��BOE�У��������к����Ķ������tan����ֵ���ó����Ķ�����Ҫ��m��ֵ�����Ƚ�Rt��BOE���ó�OB�ij��ȣ�Ȼ����ݽ��еĶԽ�����ȵó�OA=OB=OC=OD���Ӷ����m��ֵ
��3�������ı���ABCDΪ���Σ��������εĶԽ��ߴ�ֱ�һ���ƽ�֣���֪AC��BD����AC��BD����ƽ�֣���AC��x���ϣ�����BDӦ��y���ϣ����롰��B��D�ֱ��ڵ�һ�������ޡ�ì�ܣ������ı���ABCD������Ϊ���Σ�
��� 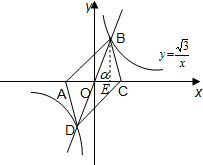 �⣺��1���߷�����������ͼ����һ�����ĶԳ�ͼ�Σ���B��D�������������뷴��������ͼ��Ľ��㣬
�⣺��1���߷�����������ͼ����һ�����ĶԳ�ͼ�Σ���B��D�������������뷴��������ͼ��Ľ��㣬
���Ե�B���D���ڵ�O�����ĶԳƣ���OB=OD����OA=OC�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ�
���ı���ABCD��ƽ���ı��Σ�
�ʴ�Ϊ��ƽ���ı��Σ�
��2���ߵ�B��p��$\sqrt{3}$����y=$\frac{\sqrt{3}}{x}$��ͼ���ϣ�
��$\sqrt{3}$=$\frac{\sqrt{3}}{p}$��
��p=1��
��B��BE��x����E����
��Rt��BOE�У���=60�㣬
��OB=2��
�֡ߵ�B��D�������������뷴��������ͼ��Ľ��㣬
���B��D����ԭ��O�����ĶԳƣ�
��OB=OD=2��
���ı���ABCDΪ���Σ���A��-m��0����C��m��0��
��OA=OB=OC=OD=2��
��m=2��
��3���ı���ABCD���������Σ��������£�
���ı���ABCDΪ���Σ���Խ���AC��BD����AC��BD����ƽ�֣�
��Ϊ��A��C������ֱ�Ϊ��-m��0������m��0����
���Ե�A��C����ԭ��O�Գƣ���AC��x���ϣ�
����BDӦ��y���ϣ�
���롰��B��D�ֱ��ڵ�һ�������ޡ�ì�ܣ�
�����ı���ABCD������Ϊ���Σ�
���� ������Ҫ�������ı����ۺ��⣬�����漰����ƽ���ı��ε��ж������Ρ����ε����ʼ����Ǻ����Ķ����֪ʶ���ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
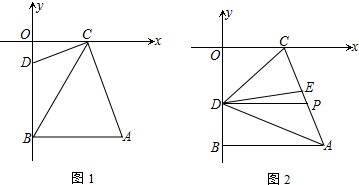
 ��ͼ��ֱ��y1=kx+2��x�ᡢy��ֱ��ڵ�A��B����C��1��a����D��b��-2����ֱ����˫����y2=$\frac{m}{x}$���������㣬����C��CE��y���ڵ�E���ҡ�BCE�����Ϊ1��
��ͼ��ֱ��y1=kx+2��x�ᡢy��ֱ��ڵ�A��B����C��1��a����D��b��-2����ֱ����˫����y2=$\frac{m}{x}$���������㣬����C��CE��y���ڵ�E���ҡ�BCE�����Ϊ1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
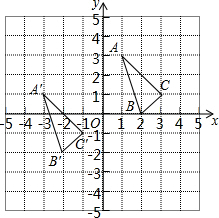 ��ABC���A'B'C'��ƽ��ֱ������ϵ�е�λ����ͼ��
��ABC���A'B'C'��ƽ��ֱ������ϵ�е�λ����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
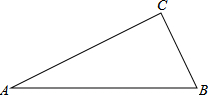 ��ͼ����Rt��ABC�У���C=90�㣬
��ͼ����Rt��ABC�У���C=90�㣬�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com