
【题目】在平面直角坐标系xOy中,四边形OABC是矩形,点B的坐标为(4,3),反比例函数y= ![]() 的图象经过点B.
的图象经过点B. 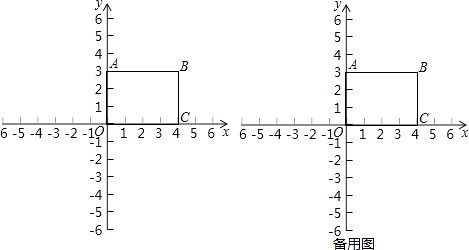
(1)求反比例函数的解析式;
(2)一次函数y=ax﹣1的图象与y轴交于点D,与反比例函数y= ![]() 的图象交于点E,且△ADE的面积等于6,求一次函数的解析式;
的图象交于点E,且△ADE的面积等于6,求一次函数的解析式;
(3)在(2)的条件下,直线OE与双曲线y= ![]() (x>0)交于第一象限的点P,将直线OE向右平移
(x>0)交于第一象限的点P,将直线OE向右平移 ![]() 个单位后,与双曲线y=
个单位后,与双曲线y= ![]() (x>0)交于点Q,与x轴交于点H,若QH=
(x>0)交于点Q,与x轴交于点H,若QH= ![]() OP,求k的值.
OP,求k的值.
【答案】
(1)解:∵反比例函数y= ![]() 的图象经过点B(4,3),
的图象经过点B(4,3),
∴ ![]() =3,
=3,
∴m=12,
∴反比例函数解析式为y= ![]()
(2)解:∵四边形OABC是矩形,点B(4,3),
∴A(0,3),C(4,0),
∵一次函数y=ax﹣1的图象与y轴交于点D,
∴点D(0,﹣1),AD=4,设点E(xE,yE),
∵△ADE的面积=6,
∴ ![]() AD|xE|=6,
AD|xE|=6,
∴xE=±3,
∵点E在反比例函数y= ![]() 图象上,
图象上,
∴E(3,4),或(﹣3,﹣4),
当E(3,4)在一次函数y=ax﹣1上时,
4=3a﹣1,
∴a= ![]() ,
,
∴一次函数解析式为y= ![]() x﹣1,
x﹣1,
当点(﹣3,﹣4)在一次函数y=ax﹣1上时,
﹣4=﹣3a﹣1,
∴a=1,
∴一次函数解析式为y=x﹣1,
综上所述一次函数解析式为y=x﹣1或y= ![]() x﹣1
x﹣1
(3)解:由(2)可知,直线OE解析式为y= ![]() x,设点P(xP,yP),取OP中点M,则OM=
x,设点P(xP,yP),取OP中点M,则OM= ![]() OP,
OP,
∴M( ![]() xP,
xP, ![]() xP),
xP),
∴Q( ![]() xP+
xP+ ![]() ,
, ![]() xP),
xP),
∴H( ![]() ,0),
,0),
∵点P、Q在反比例函数y= ![]() 图象上,
图象上,
∴xP ![]() xP=(
xP=( ![]() xP+
xP+ ![]() )
) ![]() xP,
xP,
∴xP= ![]() ,
,
∴P( ![]() ,
, ![]() ),
),
∴k= ![]() .
.
【解析】(1)利用待定系数法即可解决.(2)设点E(xE , yE),由△ADE的面积=6,得 ![]() AD|xE|=6,列出方程即可解决.(3)设点P(xP , yP),取OP中点M,则OM=
AD|xE|=6,列出方程即可解决.(3)设点P(xP , yP),取OP中点M,则OM= ![]() OP,则M(
OP,则M( ![]() xP ,
xP , ![]() xP),Q(
xP),Q( ![]() xP+
xP+ ![]() ,
, ![]() xP),列出方程求出xP即可解决问题.
xP),列出方程求出xP即可解决问题.
【考点精析】本题主要考查了矩形的性质和坐标与图形变化-平移的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
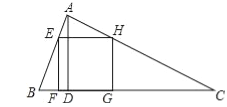
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)已知a+b=2,ab=2,求a3b+2a2b2+ab3的值.
(2)求(2x﹣y)(2x+y)﹣(2y+x)(2y﹣x)的值,其中x=2,y=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地计划用120~180天(含120与180天)的时间建设一项水利工程,工程需要运送的土石方总量为360万立方米.
(1)写出运输公司完成任务所需的时间y(单位:天)与平均每天的工作量x(单位:万立方米)之间的函数关系式,并给出自变量x的取值范围;
(2)由于工程进度的需要,实际平均每天运送土石方比原计划多5000立方米,工期比原计划减少了24天,原计划和实际平均每天运送土石方各是多少万立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题,例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值. 解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题
(1)若△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0,请问△ABC是什么形状?说明理由.
(2)若x2+4y2﹣2xy+12y+12=0,求xy的值.
(3)已知a﹣b=4,ab+c2﹣6c+13=0,则a+b+c= .
查看答案和解析>>
科目:初中数学 来源: 题型:
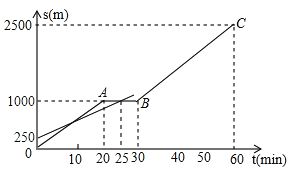
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:
销售量n(件) | n=50﹣x |
销售单价m(元/件) | 当1≤x≤20时,m=20+ |
当21≤x≤30时, |
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛,赛后组委会整理参赛同学的成绩,并制作了如图不完整的频数分布表和频数分布直方图

请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= ;请补全频数分布直方图;
(2)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是 ;
(3)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com