
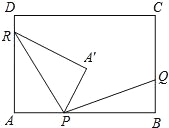
【题目】如图,在矩形ABCD中,AB=8k,BC=5k(k为常数,且k>0),动点P在AB边上(点P不与A、B重合),点Q、R分别在BC、DA边上,且AP:BQ:DR=3:2:1.点A关于直线PR的对称点为A′,连接PA′、RA′、PQ.
(1)若k=4,PA=15,则四边形PARA′的形状是 ;
(2)设DR=x,点B关于直线PQ的对称点为B′点.
①记△PRA′的面积为S1,△PQB′的面积为S2.当S1<S2时,求相应x的取值范围及S2﹣S1的最大值;(用含k的代数式表示)
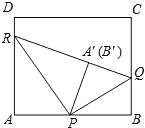
②在点P的运动过程中,判断点B′能否与点A′重合?请说明理由.
【答案】(1)正方形;(2)当x=![]() 时,S2﹣S1有最大值,最大值为
时,S2﹣S1有最大值,最大值为![]() k2.(3)点B′不能与点A′重合.理由见解析.
k2.(3)点B′不能与点A′重合.理由见解析.
【解析】
试题分析:(1)先证明四边形PARA′是菱形,再根据∠A=90°,可以推出四边形PARA′是正方形.
(2)①分别求出S1,S2,根据S1<S2,确定自变量取值范围,再构建S2﹣S1关于x的二次函数,根据二次函数的性质即可解决问题.
②点B'不能与点A'重合,利用反证法即可证明.
试题解析:(1)∵k=4,PA=15,AP:BQ:DR=3:2:1,∴DR=5,BC=AD=20,AR=AP=15,∵A、A′关于PR对称,∴RA=RA′=PA=PA′,∴四边形PARA′是菱形,∵∠A=90°,∴四边形PARA′是正方形.
故答案为正方形;
(2)①由题意可知,BQ=2x,PA=3x,AR=5k﹣x,BP=8k﹣3x,
∵S1=S△PRA=![]() ARAP=
ARAP=![]() (5k﹣x)3x=﹣
(5k﹣x)3x=﹣![]() x2+
x2+![]() kx,
kx,
S2=S△PQB=![]() BPBQ=
BPBQ=![]() (8k﹣3x)2x=﹣3x2+8kx,
(8k﹣3x)2x=﹣3x2+8kx,
由S1<S2可得,﹣![]() x2+
x2+![]() <﹣3x2+8kx,∵x>0,∴x取值范围为0<x<
<﹣3x2+8kx,∵x>0,∴x取值范围为0<x<![]() k,
k,
∴S2﹣S1=﹣![]() x2+
x2+![]() kx=﹣
kx=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() k2,
k2,
∴当x=![]() 时,S2﹣S1有最大值,最大值为
时,S2﹣S1有最大值,最大值为![]() k2.
k2.
②点B'不能与点A'重合.理由如下:
如图,假设点B'与点A'重合,则有∠APR+∠A'PR+∠B'PQ+∠BPQ=180°,
由对称的性质可得,∠A'PR=∠APR,∠![]() ×180°=90°,
×180°=90°,
由∠A=90°可得,∠APR+∠PRA=90°,∴∠PRA=∠BPQ,又∵∠A=∠B=90°
∴Rt△PAR∽Rt△QBP,∴![]() ,即PABP=ARQB.
,即PABP=ARQB.
∴3x(8k﹣3x)=(5k﹣x)2x,解得,x1=0(不合题意舍去),x2=2k,
又∵PA=PA',PB=PB'=PA',∴PA=PB,∴3x=8k﹣3x,解得x=![]() k≠2k,
k≠2k,
故点B'不能与点A'重合.


科目:初中数学 来源: 题型:
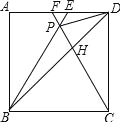
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:①△BDE∽△DPE;②![]() ;③
;③![]() =PHPB;④tan∠DBE=
=PHPB;④tan∠DBE=![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
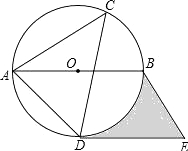
【题目】如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm,
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)试求∠DAE的度数;
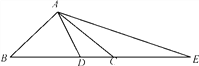
(2)如果把原题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。并证明这个命题(只写出一种情况)①AB=AC; ②DE=DF; ③BE=CF。(在已知和求证中,填写正确序号)
已知:EG∥AF,_______,_________.
求证:__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com