
【题目】已知在平面直角坐标系xOy中,抛物线![]() (b为常数)的对称轴是直线x=1.
(b为常数)的对称轴是直线x=1.
(1)求该抛物线的表达式;
(2)点A(8,m)在该抛物线上,它关于该抛物线对称轴对称的点为A',求点A'的坐标;
(3)选取适当的数据填入下表,并在如图5所示的平面直角坐标系内描点,画出该抛物线.

科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两个不透明的盒子,
两个不透明的盒子,![]() 盒中装有红色、黄色、蓝色卡片各1张,
盒中装有红色、黄色、蓝色卡片各1张,![]() 盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从
盒中装有红色、黄色卡片各1张,这些卡片除颜色外都相同.现分别从![]() 、
、![]() 两个盒子中任意摸出一张卡片.
两个盒子中任意摸出一张卡片.
(1)从![]() 盒中摸出红色卡片的概率为______;
盒中摸出红色卡片的概率为______;
(2)用画树状图或列表的方法,求摸出的两张卡片中至少有一张红色卡片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
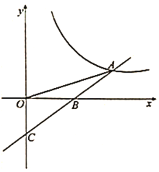
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
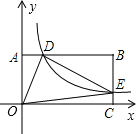
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y=![]() (x>0)的图象与AB相交于点D.与BC相交于点E,且BD=3,AD=6,△ODE的面积为15,若动点P在x轴上,则PD+PE的最小值是_____.
(x>0)的图象与AB相交于点D.与BC相交于点E,且BD=3,AD=6,△ODE的面积为15,若动点P在x轴上,则PD+PE的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行,某自行车店在销售某型号自行车时,以高出进价的50%标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出50辆;若每辆自行车每降价20元,每月可多售出5辆,求该型号自行车降价多少元时,每月可获利30000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 汕头国际马拉松赛事设有“马拉松(
汕头国际马拉松赛事设有“马拉松(![]() 公里)”,“半程马拉松(
公里)”,“半程马拉松(![]() 公里)”,“迷你马拉松(
公里)”,“迷你马拉松(![]() 公里)”三个项目,小红和小青参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
公里)”三个项目,小红和小青参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到三个项目组.
(1)小红被分配到“马拉松(![]() 公里)”项目组的概率为___________.
公里)”项目组的概率为___________.
(2)用树状图或列表法求小红和小青被分到同一个项目组进行志愿服务的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
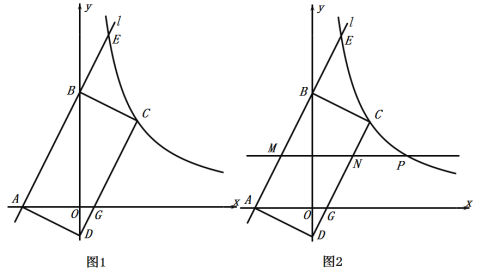
如图1,平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,
,![]() .双曲线
.双曲线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)在图1中以线段![]() 为边作矩形
为边作矩形![]() ,使顶点
,使顶点![]() 在第一象限、顶点
在第一象限、顶点![]() 在
在![]() 轴负半轴上.线段
轴负半轴上.线段![]() 交
交![]() 轴于点
轴于点![]() .直接写出点
.直接写出点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(3)如图2,在(2)题的条件下,已知点![]() 是双曲线
是双曲线![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的平行线分别交线段
轴的平行线分别交线段![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
请从下列![]() ,
,![]() 两组题中任选一组题作答.我选择组题.
两组题中任选一组题作答.我选择组题.
A.①当四边形![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
B.①当四边形![]() 成为菱形时,求点
成为菱形时,求点![]() 的坐标;
的坐标;
②在①的条件下,连接![]() ,
,![]() .坐标平面内是否存在点
.坐标平面内是否存在点![]() (不与点
(不与点![]() 重合),使以
重合),使以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 全等?若存在,直接写出点
全等?若存在,直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a、b、c是常数,a<0)经过点A(-1,0)、B(3,0),顶点为C,则下列说法正确的个数是( )
①当-1<x<3时,ax2+bx+c>0;②当△ABC是直角三角形,则a=-![]() ;
;
③若m≤x≤m+3时,二次函数y=ax2+bx+c的最大值为am2+bm+c,则m≥3.
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图像如图所示,它的对称轴为直线
的图像如图所示,它的对称轴为直线![]() ,与
,与![]() 轴交点的横坐标分别为
轴交点的横坐标分别为![]() ,
,![]() ,且
,且![]() .下列结论中:①
.下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根;⑤
有两个相等的实数根;⑤![]() .其中正确的有( )
.其中正确的有( )
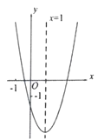
A.②③⑤B.②③C.②④D.①④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com