
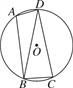
【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
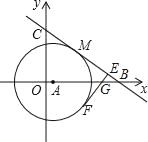
【题目】如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=﹣![]() x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
(1)直接写出b的值和点B的坐标;
(2)求点A的坐标和圆的半径;
(3)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个两位数,十位数字是![]() ,个位数字是
,个位数字是![]() ,总有
,总有![]() ,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,
,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,![]() ,
,![]() ,所以25和7分别是43的“平方和数”与“平方差数”。
,所以25和7分别是43的“平方和数”与“平方差数”。
(1)76的“平方和数”是_____________,“平万差数”是____________.
(2)5可以是___________的“平方差数”.
(3)若一个数的“平方和数”是10,“平方差数”是8,则这个数是______.
(4)若一个数的“平方和数”,与它的“平方差数”相等,那么这个数满足什么特征?为什么?(写出说明过程)
(5)若一个数的“平方差数”等子它十位上的数与个位上的数差的十倍,此时,我们把它叫做“凑整数”,请你写出两个这样的凑整数_____________,__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适宜采用全面调查方式(普查)的是( )
A. 对襄阳市中学生每天课外读书所用时间的调查
B. 对全国中学生心理健康现状的调查
C. 对七年级(2)班学生![]() 米跑步成绩的调查
米跑步成绩的调查
D. 对市面某品牌中性笔笔芯使用寿命的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC,记S=S四边形MAOC﹣S△BOC,求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2,点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△DBC都是边长为2的等边三角形.

(1)以图1中的某个点为旋转中心,旋转△DBC,就能使△DBC与△ABC重合,则满足题意的点为: (写出符合条件的所有点);
(2)将△DBC沿BC方向平移得到△D1B1C1,如图2、图3,则四边形ABD1C1是平行四边形吗?证明你的结论;
(3)在(2)的条件下,当BB1= 时,四边形ABD1C1为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3.
(1)画出这个函数的图象;
(2)根据图象,直接写出;
①当函数值y为正数时,自变量x的取值范围;
②当﹣2<x<2时,函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种蔬菜的价格随季节变化如下表,根据表中信息,下列结论错误的是( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
价格 | 5.00 | 5.50 | 5.00 | 4.80 | 2.00 | 1.50 | 1.00 | 0.90 | 1.50 | 3.00 | 2.50 | 3.50 |
A. ![]() 是自变量,
是自变量,![]() 是因变量
是因变量
B. 2月份这种蔬菜价格最高,为5.50元/千克
C. 2-8月份这种蔬菜价格一直在下降
D. 8-12月份这种蔬菜价格一直在上升
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:①0是最小的整数;②有理数不是正数就是负数;③正整数、负整数、正分数、负分数统称为有理数;④非负数就是正数;④![]() 不仅是有理数,而且是分数;⑤
不仅是有理数,而且是分数;⑤![]() 是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
是无限不循环小数,所以不是有理数;⑥无限小数不都是有理数;⑦正数中没有最小的数,负数中没有最大的数.其中错误的说法的个数为( )
A. 7个B. 6个C. 5个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com