
【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2![]() ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.



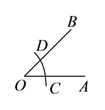
(Ⅰ)如图1,求∠DAO的大小及线段DE的长;
(Ⅱ)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3![]() .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
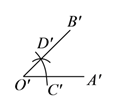
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
【答案】(Ⅰ)∠DAO=60°,DE=2; (Ⅱ)①GH=6,DG=﹣3+![]() ;②F(﹣5﹣
;②F(﹣5﹣![]() ,0).
,0).
【解析】解:(Ⅰ)∵A(﹣2,0),D(0,2![]() )∴AO=2,DO=2
)∴AO=2,DO=2![]() ,∴tan∠DAO=
,∴tan∠DAO=![]() =
=![]() ,
,
∴∠DAO=60°,∴∠ADO=30°,∴AD=2AO=4,∵点E为线段AD中点,∴DE=2;
(Ⅱ)①如图2,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DGE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,
∴∠EOF′=∠AEO,∴AD∥OF′,∴∠OF′E=∠DEH,∴∠DEH=∠DGE,
∵∠DEH=∠EDG,∴△DHE∽△DEG,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DG=x,则DH=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,∴DG=﹣3+
,∴DG=﹣3+![]() .
.
②如图3,

过点E作EM⊥CD,∴CD∥AB,∴∠EDM=∠DAB=60°,∴EM=DEsin60°=![]() ,∴GH=6,
,∴GH=6,
∵CD∥AB,∴∠DHE=∠OFE,
∵△OEF′是△OEF关于直线OE的对称图形,∴△OEF′≌△OEF,∴∠OFE=∠OF′E,
∵点E是AD的中点,∴OE=![]() AD=AE,
AD=AE,
∵∠EAO=60°,∴△EAO是等边三角形,∴∠EOA=60°,∠AEO=60°,
∵△OEF′≌△OEF,∴∠EOF′=∠EOA=60°,∴∠EOF′=∠AEO,∴AD∥OF′,
∴∠OF′E=∠DEH,∴∠DEG=∠DHE,
∵∠DEG=∠EDH,∴△DGE∽△DEH,∴![]() ,∴DE2=DG×DH,
,∴DE2=DG×DH,
设DH=x,则DG=x+6,∴4=x(x+6),∴x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ,
,
∴DH=﹣3+![]() .∴DG=3+
.∴DG=3+![]() ∴DG=AF=3+
∴DG=AF=3+![]() ,∴OF=5+
,∴OF=5+![]() ,∴F(﹣5﹣
,∴F(﹣5﹣![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(本题8分) 求一个正数的算术平方根,有些数可以直接求得,如![]() ,有些数则不能直接求得,如
,有些数则不能直接求得,如![]() ,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
,但可以通过计算器求. 还有一种方法可以通过一组数的内在联系,运用规律求得,请同学们观察下表:
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)表中所给的信息中,你能发现什么规律?(请将规律用文字表达出来)
(2)运用你发现的规律,探究下列问题:已知![]()
![]() 1.435,求下列各数的算术平方根:
1.435,求下列各数的算术平方根:
①0.0206![]() ; ②20600
; ②20600![]() ;
;
(3)根据上述探究过程类比研究一个数的立方根已知![]()
![]() 1.260,则
1.260,则![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国计划在2020年左右发射火星探测卫星,据科学研究,火星距离地球的最近距离约为55000000千米.用科学记数法表示数据55000000为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,求作
,求作![]() ,使
,使![]() ,根据下图填空:
,根据下图填空:
作法:(![]() )作射线__________;
)作射线__________;
(![]() )以点____为圆心,以任意长为半径画弧,交
)以点____为圆心,以任意长为半径画弧,交![]() 于点_____,交______于点_____;
于点_____,交______于点_____;
(![]() )以点_____为圆心,以______长为半径画弧,交
)以点_____为圆心,以______长为半径画弧,交![]() 于点_______;
于点_______;
(![]() )以点______为圆心,以______长为半径画弧,交前面的弧于点
)以点______为圆心,以______长为半径画弧,交前面的弧于点![]() ;
;
(![]() )过点_______作射线_______,则________就是所求作的角.
)过点_______作射线_______,则________就是所求作的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(1)写出月产销量y(个)与销售单价x (元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com