
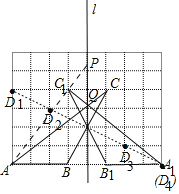
����Ŀ����ͼ���ڳ���Ϊ1����λ���ȵ�С��������ɵ������������У���ABC����������A��B��C���ڸ���ϣ�
��1����ͼ�л������ABC����ֱ��l����ԳƵġ�A1B1C1��
��2����ֱ��l���ҳ�һ��P��ʹ��|PA��PC|��ֵ���������ͼ�ۼ���������ĸP��
��3����ֱ��l���ҳ�һ��Q��ʹ��QA+QC1��ֵ��С����������ͼ�ۼ���������ĸQ��
��4���������������д����� ������㣬ʹ�øø����B��C���㹹����BCΪ�ױߵĵ��������Σ�

���𰸡���1������������2������������3������������4��4
��������
��1���ֱ�����A��B��C�Ķ�Ӧ��A1��B1��C1���ɣ�
��2������AC1���ӳ�AC1��ֱ��l�ڵ�P����P��Ϊ����
��3��ֱ��AC��ֱ��l�Ľ���Q��Ϊ����
��4�����߶�BC�Ĵ�ֱƽ���ߣ���ͼD1��D2��D3��D4��Ϊ����
�⣺��1����A1B1C1��ͼ��ʾ��
�ɶԳƵ����ʣ��ֱ�����A��B��C�Ķ�Ӧ��A1��B1��C1��˳������A1B1��A1 C1��B1C1��
�õ���A1B1C1����ABC����ֱ��l����Գƣ�
��2����C��C1����ֱ��l�Գƣ�
��PC=PC1��
��|PA��PC|=|PA��PC1|����P��A��C1���㹲��ʱ��|PA��PC1|ȡ�����ֵ����|PA��PC|��ֵ���
������AC1���ӳ�AC1��ֱ��l�ڵ�P����P��Ϊ����
��3����C��C1����ֱ��l�Գƣ�
��QC=QC1��
��QA+QC1=QA+QC����A��Q��C���㹲��ʱ��QA+QCȡ����Сֵ����QA+QC1��ֵ��С��
��ֱ��AC��ֱ��l�Ľ���Q��Ϊ����
��4���߹�����BCΪ�ױߵĵ��������Σ�
����������εĶ������߶�BC�Ĵ�ֱƽ�����ϣ�
�����߶�BC�Ĵ�ֱƽ���ߣ���ͼD1��D2��D3��D4��Ϊ����4����㣻
�ʴ�Ϊ4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD=10��EΪAB��һ�㣬��AE= ![]() AB=a������DE��F��DE�е㣬����BF����BFΪֱ������O��
AB=a������DE��F��DE�е㣬����BF����BFΪֱ������O��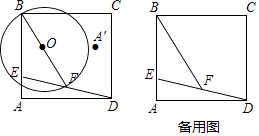
��1����a�Ĵ���ʽ��ʾDE2= �� BF2=��
��2����֤����O�ع�BC���е㣻
��3������O�����ABCD�������ڵ�ֱ������ʱ����a��ֵ��
��4����A����ֱ��BF�ĶԳƵ�A�䣬��A�����ھ���ABCD�ڲ����������߽磩����a��ȡֵ��Χ �� ��ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AB=AC=5��cos��ABC=0.6������ABC�Ƶ�C˳ʱ����ת���õ���A1B1C��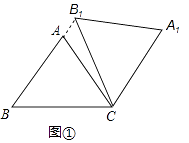
��1����ͼ1������B1���߶�BA�ӳ�����ʱ������֤��BB1��CA1�������AB1C�������
��2����ͼ2����E��BC�ߵ��е㣬��FΪ�߶�AB�ϵĶ��㣬�ڡ�ABC�Ƶ�C˳ʱ����ת�����У���F�Ķ�Ӧ����F1 �� ���߶�EF1���ȵ����ֵ����Сֵ�IJ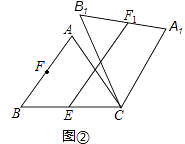
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ݮ��ֲ�������ز�����������ժ����ݮ���ּӹ�����������ֱ���������ҵ��춼����������ֱ��������40Ԫ/�����ӹ�������130Ԫ/��(�������)����֪���ع�Ӷ20��������ÿ������ֻ�ܲ����ժ�ͼӹ��е�һ�����ÿ��ÿ����Բ�ժ70���ӹ�35�����谲��x�����˲�ժ��ݮ��ʣ�µĹ��˼ӹ���ݮ��
(1)������һ�������������ΪyԪ����y��x�ĺ�����ϵʽ��
(2)������η��乤��������ʹһ��������������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,A,B����ֱ��ʾ������¥���ڵ�λ��,ֱ��a��ʾ��ˮ�ܹܵ�,ֱ��b��ʾ��ú���ܹܵ�.��Ҫ���������ܹܵ��Ϸֱ���һ�����ӵ�,��װ�ֹܵ���ˮ��ú�����͵�A,B������¥,Ҫ��ʹ������������¥����ˮ�ֹܵ�����ú���ֹܵ����������.ͼ��,��A'�ǵ�A����ֱ��b�ĶԳƵ�,A'B�ֱ�ֱ��b,a�ڵ�C,D;��B'�ǵ�B����ֱ��a�ĶԳƵ�,B'A�ֱ�ֱ��b,a�ڵ�E,F.�����Ҫ�����ˮ����ú���ֹܵ������ӵ�������
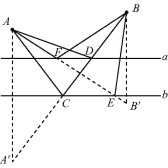
A. F��C B. F��E C. D��C D. D��E
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ�����ˮ������ͼ��ˮ����A���ر�ƫ��65������B�壬��B���ر�ƫ��25������C��ˮ����C����ʲô�����������Ա�����AB�ķ���һ�£�
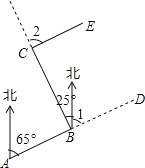
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ԡ�ѧ����ѧУ���ֻ�Ӱ��ѧϰ������������˵��飬��������˲���ѧ�����Դ�����Ŀ�����Ϊ���������û��Ӱ�졢Ӱ�첻��Ӱ��ܴ������������Ƴ����²�������ͳ�Ʊ�������ͳ��ͼ������ͳ��ͼ���ṩ����Ϣ������������⣺
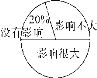
����ͳ�Ʊ����£�
���� | û��Ӱ�� | Ӱ�첻�� | Ӱ��ܴ� |
ѧ������(��) | 20 | 30 | a |
��1��ͳ�Ʊ��е�a������������
��2������ݱ��е����ݣ�̸̸��Ŀ�����������2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�CD��AB������ΪD����E��BC�ϣ�EF��AB������ΪF.

(1) CD��EFƽ����Ϊʲô��
(2)�����1=��2���ҡ�3=115�������ACB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y=![]() �ڵ�һ����ͼ������OABC�Խ��ߵĽ���E����BC���ڵ�D������B������Ϊ��6��4����
�ڵ�һ����ͼ������OABC�Խ��ߵĽ���E����BC���ڵ�D������B������Ϊ��6��4����
��1����E������꼰k��ֵ��
��2�����OCD�������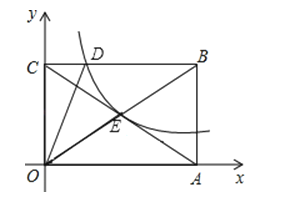
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com