
【题目】如图,某电视台的娱乐节目《周末打放送》有这样的翻奖牌游戏,数字的背面写有祝福语或奖金数,游戏规则是:每翻动正面一个数字,看看反面对应的内容,就可知是得奖还是得到温馨祝福.
1 | 2 | 3 |
4 | 5 | 6 |
7 | 8 | 9 |
正面
祝你开心 | 万事如意 | 奖金800元 |
身体健康 | 心想事成 | 奖金500元 |
奖金200元 | 生活愉快 | 谢谢参与 |
反面
计算:
(1)“翻到奖金800元”的概率;
(2)“翻到奖金”的概率;
(3)“翻不到奖金”的概率.
【答案】
(1)解:根据题意分析可得:每次翻动正面一个数字共9种情况,其中有1种情况是“翻到奖金800元”,故其“翻到奖金800元”的概率为 ![]()
(2)解:根据题意分析可得:每次翻动正面一个数字共9种情况,其中有3种情况是“翻到奖金”;“翻到奖金“的概率为 ![]() =
= ![]()
(3)解:根据题意分析可得:每次翻动正面一个数字共9种情况,其中有6种情况是“翻不到奖金”“翻不到奖金”的概率为 ![]() =
= ![]()
【解析】根据概率的求法,找准两点:1、全部情况的总数;2、符合条件的情况数目;二者的比值就是其发生的概率.
【考点精析】利用概率公式对题目进行判断即可得到答案,需要熟知一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三角形三条内角平分线的交点叫做三角形的内心;
性质:内心到三角形三边的距离相等.
如图1,点 ![]() 为
为 ![]() 的内心,
的内心, ![]() 于
于 ![]() ,
, ![]() 于E,
于E, ![]() 于
于 ![]() ,则有
,则有 ![]() .
.
问题:如何求 ![]() 的值呢?
的值呢?
探究:
(1)小明思路:设△ABC的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,
, ![]() 的面积为
的面积为 ![]() ,利用
,利用 ![]() 可求
可求 ![]() .
.
①图1中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,请你根据小明的思路求出
,请你根据小明的思路求出 ![]() 的值;
的值;
②如图2,△ABC中, ![]() ,设
,设 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为 △ABC的内心,
为 △ABC的内心, ![]() 于
于 ![]() ,
, ![]() 于E,
于E, ![]() 于
于 ![]() .若设
.若设 ![]() ,请用含
,请用含 ![]() ,
, ![]() ,
, ![]() 的式子表示
的式子表示 ![]() ;
;
(2)小亮思路:“凡角平分处,必有轴对称”. 如图2,易得: ![]() ,
, ![]() ,
, ![]() . 请你根据小亮的思路,用含
. 请你根据小亮的思路,用含 ![]() ,
, ![]() ,
, ![]() 的式子表示
的式子表示 ![]() ;
;
(3)①根据上述所列两式,求证: ![]() ;
;
②应用:已知一个直角三角形的两直角边长分别为 ![]() 和
和 ![]() ,求该三角形的内心到任意一边的距离
,求该三角形的内心到任意一边的距离 ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
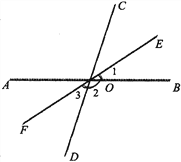
【题目】如图所示,直线AB、CD相交于点O,且∠BOC=80°,OE平分∠BOC.OF为OE的反向延长线.求∠2和∠3的度数,并说明OF是否为∠AOD的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有22名工人,每人每天可以生产600个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应如何安排生产螺钉和螺母的工人各多少名?设该车间每天有x人生产螺钉,则根据题意列出的方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,点B1、点C1的坐标分别为(1,0),![]() ,将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2.将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得△OBnCn.
,将△OB1C1绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB2=OC1,得到△OB2C2.将△OB2C2绕原点O逆时针旋转60°,再将其各边都扩大为原来的m倍,使OB3=OC2,得到△OB3C3,如此下去,得△OBnCn.
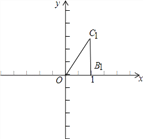
(1)m的值是___;
(2)△OB2016C2016中,点C2016的坐标:______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com