
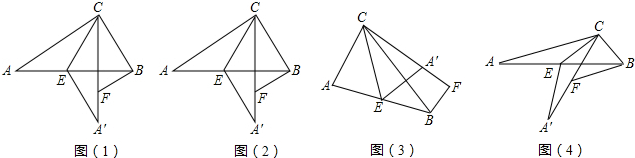
分析 (1)根据翻折得出AC=A'C,利用含30°的直角三角形的性质进行解答即可;
(2)连接A′B,根据翻折的性质可得A′E=AE,A′C=AC,∠A=∠CA′E,根据中点定义可得AE=BE,从而得到BE=A′E,然后根据等边对等角可得∠EA′B=∠EBA′,根据两直线平行,内错角相等可得∠A=∠ABF,然后求出∠FA′B=∠FBA′,根据等角对等边可得A′F=BF;
(3)图(3)连接A′B,根据翻折的性质可得A′E=AE,A′C=AC,∠A=∠CA′E,根据中点定义可得AE=BE,从而得到BE=A′E,然后根据等边对等角可得∠EA′B=∠EBA′,根据两直线平行,内错角相等可得∠A=∠ABF,然后求出∠FA′B=∠FBA′,根据等角对等边可得A′F=BF,再根据A′C=CF-A′F整理即可得证;
(4)连接A′B,过点F作FG⊥BC于G,根据两直线平行,同旁内角互补求出∠CBF=60°,然后解直角三角形求出BG、FG,再求出CG,然后利用勾股定理列式求出CF,再根据AC=CF+BF代入数据计算即可得解.
解答 解:(1)将△ABC沿CE所在的直线折叠得△A′EC,
∴AC=A'C,
∵∠ACB=90°,∠A=30°,BC=$\sqrt{3}$,
∴AC=A'C=3,
∵BC=$\sqrt{3}$,
∴CF=2,
∴A′F=3-2=1;
(2)如图(2),连接A′B,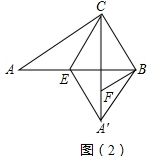
由翻折的性质得,A′E=AE,A′C=AC,∠A=∠CA′E,
∵点E为边AB的中点,
∴AE=BE,
∴BE=A′E,
∴∠EA′B=∠EBA′,
∵BF∥AC,
∴∠A+∠ABF=180°,
∵∠CA′E+∠EA′F=180°,
∴∠ABF=∠EA′F,
∵∠FA′B=∠EA′F-∠EA′B,
∠FBA′=∠ABF-∠EBA′,
即∠FA′B=∠FBA′,
∴A′F=BF=a;
(3)如图(3),连接A′B,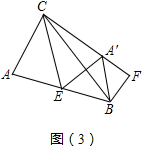
由翻折的性质得,A′E=AE,A′C=AC,∠A=∠CA′E,
∵点E为边AB的中点,
∴AE=BE,
∴BE=A′E,
∴∠EA′B=∠EBA′,
∵BF∥AC,
∴∠A+∠ABF=180°,
∵∠CA′E+∠EA′F=180°,
∴∠ABF=∠EA′F,
∵∠FA′B=∠EA′F-∠EA′B,
∠FBA′=∠ABF-∠EBA′,
即∠FA′B=∠FBA′,
∴A′F=BF,
∵A′C=CF-A′F,
∴AC=CF-BF;
故答案为:AC=CF-BF;
(4)解:如图(4),连接A′B,过点F作FG⊥BC于G,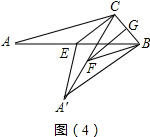
∵BF∥AC,∠ACB=120°,
∴∠CBF=180°-120°=60°,
∴BG=BF•cos60°=8×$\frac{1}{2}$=4,FG=BF•sin60°=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
∴CG=BC-BG=5-4=1,
在Rt△CGF中,CF=$\sqrt{F{G}^{2}+C{G}^{2}}=\sqrt{(4\sqrt{3})^{2}+{1}^{2}}=7$,
∴AC=BF+CF=8+7=15.
故答案为:15
点评 本题考查了翻折变换,平行线的性质,等边对等角的性质,解直角三角形,勾股定理的应用,作辅助线构造出等腰三角形是解题的关键,也是本题的难点.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
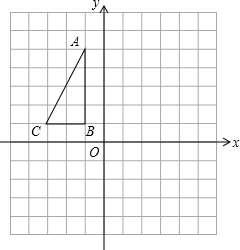 如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(-1,5)、B(-1,1)、C(-3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2
如图,在平面直角坐标系中,ABC的顶点的坐标分别为A(-1,5)、B(-1,1)、C(-3,1).将△ABC向右平移2个单位、再向下平移4个单位得到△A1B1C1;将△ABC绕原点O旋转180°得到△A2B2C2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=-1,c=3 | B. | a=-1,b=1,c=3 | C. | a=1,b=-1,c=-3 | D. | a=-1,b=1,c=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某洗衣机洗涤衣服时,经历了进水,清洗,排水脱水四个连续的过程,其中进水,清洗,排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图折线图所示,已知清洗时间为11分钟,排水时间为2分钟,则排水结束时洗衣机中剩下的水量为$\frac{82}{3}$升.
某洗衣机洗涤衣服时,经历了进水,清洗,排水脱水四个连续的过程,其中进水,清洗,排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图折线图所示,已知清洗时间为11分钟,排水时间为2分钟,则排水结束时洗衣机中剩下的水量为$\frac{82}{3}$升.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com