
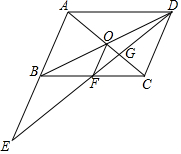
 已知E为平行四边形ABCD中AB边上一点,且BE=AB,连接DE交BC于F,交AC于G.
已知E为平行四边形ABCD中AB边上一点,且BE=AB,连接DE交BC于F,交AC于G.分析 (1)根据平行线的性质得出∠E=∠CDF,∠EBF=∠DCF,结合BE=CD=AB即可判断三角形的全等.
(2)根据题意可判断出OF是△ABC的中位线,从而可判断出数量及位置关系.
解答 解:(1)证明:
∵四边形ABCD是平行四边形,
∵AB∥CD,AB=CD,
∴∠E=∠CDF,∠EBF=∠DCF,
又∵BE=AB,
∴BE=DC,
在:△BEF和△CDF中,
$\left\{\begin{array}{l}{∠EBD=∠DCF}\\{∠E=∠CDF}\\{BE=DC}\end{array}\right.$
∴△BEF≌△CDF(AAS);
(2)OF=$\frac{1}{2}$AB,OF∥AB.理由如下:
∵OA=OC,BF=FC,
∴OF是△ABC的中位线.
∴OF=$\frac{1}{2}$AB,OF∥AB.
点评 此题考查了平行四边形的性质、全等三角形的判定及性质,难度一般,解答本题的关键是根据题意得出OF是△ABC的中位线.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
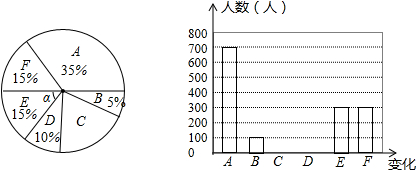
| 种类 | A | B | C | D | E | F |
| 变化 | 有利于延缓社会老龄化现象 | 导致人口暴增 | 提升家庭抗风险能力 | 增大社会基本公共服务压力 | 缓解男女比例不平衡的现象 | 促进人口与社会、资源、环境的协调可持续发展 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com