
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图N48中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
(1)求函数y=-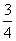 x+3的坐标三角形的三条边长;
x+3的坐标三角形的三条边长;
(2)若函数y=-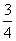 x+b(b为常数)的坐标三角形周长为16,求此三角形的面积.
x+b(b为常数)的坐标三角形周长为16,求此三角形的面积.
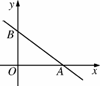
图N48
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
如图6514,将一个有45°角的三角板的直角顶点放在一张宽为3 cm的矩形纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,则三角板最大边的长为( )
A.3 cm B. 6 cm C.3 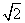 cm D.6
cm D.6 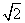 cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
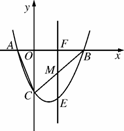
如图N212,在平面直角坐标系中,直线y=-3x-3与x轴交于点A,与y轴交于点C.抛物线y=x2+bx+c经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图N41,已知AB∥CD,BE平分∠ABC,且交CD于D点, ∠CDE=150°,则∠C为( )
A.120° B.150°
C.135° D.110°
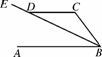
查看答案和解析>>
科目:初中数学 来源: 题型:
某中学为了让学生的跳远在中考体育测试中取得满意的成绩,在锻炼一个月后,学校对九年级一班的45名学生进行测试,成绩如下表:
| 跳远成绩(cm) | 160 | 170 | 180 | 190 | 200 | 220 |
| 人数 | 3 | 9 | 6 | 9 | 15 | 3 |
这些运动员跳远成绩的中位数和众数分别是( )
A. 190,200 B.9,9 C.15,9 D.185,200
查看答案和解析>>
科目:初中数学 来源: 题型:
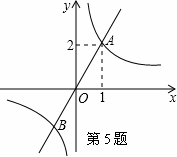
如图,函数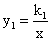 与
与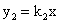 的图象相交于点A(1,2)和点B,当y1>y2时的变量x的取值范围是( )
的图象相交于点A(1,2)和点B,当y1>y2时的变量x的取值范围是( )
A、x>1 B、-1<x<0 C、-1<x<0或x>1 D、x<-1或0<x<1
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,抛物线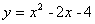 与直线
与直线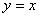 交于点A、B,M是抛物线上一个动点,连接OM。
交于点A、B,M是抛物线上一个动点,连接OM。
(1) 当M为抛物线的顶点时,求△OMB的面积;
(2) 当点M在抛物线上,△OMB的面积为10时,求点M的坐标;
(3) 当点M在直线AB的下方且在抛物线对称轴的右侧,M运动到何处时,△OMB的面积最大;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com