练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．若4x2-ax+$\frac{1}{9}$是一个完全平方式，则a=±$\frac{4}{3}$．

    分析 符合a2+2ab+b2形式的式子叫完全平方式，要明确，常数项是一次项系数一半的平方，进而求出即可．

    解答 解：∵4x2-ax+$\frac{1}{9}$是一个完全平方式，
    ∴-a=±2×2×$\frac{1}{3}$，
    ∴a=±$\frac{4}{3}$．
    故答案为：$±\frac{4}{3}$．

    点评 本题考查了完全平方式，解题的关键是知道常数项是一次项系数一半的平方．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．如图所示，矩形ABCD中，AB=$\sqrt{6}$，AD=5，在AD上是否存在一点P，使∠BPC=90°？如果存在，试求出AP的长；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

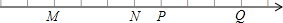
    17．数轴上标出若干个整数点，每相邻两点相距一个单位，点M、N、P、Q分别表示整数m，n，p，q，且q-3m=13，则原点O在（　　）位置．
    A．点MB．点NC．点PD．点Q

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

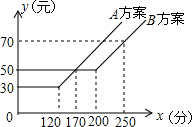    14．某移动通讯公司提供的A、B两种方案通讯费用y（元）与通话时间x（分）之间的关系如图所示．以下说法：
    ①若通话时间少于120分，则A方案比B方案便宜20元；
    ②若通话时间超过200分，则B方案比A方案便宜；
    ③若通话费用为60元，则B方案比A方案的通话时间多；
    ④若两种方案通讯费用相差10元，则通话时间是145分或185分；
    其中准确的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．一次作业中，小华作业中，小华做了这样一道，以下是他的解题过程：
    题目：当m为何值时，关于x的方程x2+（m+2）x+2m-1=0的两根互为相反数？
    解：因为：关于x的方程x2+（m+2）x+2m-1=0的两根互为相反数；
    所以：$\left\{\begin{array}{l}{{k}^{2}+（m+2）k=2m-1=0（1）}\\{（-k）^{2}+（m+2）（-k）+2m-1=0（2）}\end{array}\right.$
    （1）式减（2）式得：2（m+2）k=0
    所以：m=-2或k=0；把k=0代入（1）式，得m=$\frac{1}{2}$
    所以：m=-2或m=$\frac{1}{2}$
    （1）请你把m的值代入原方程；分别求出这两种情况下，关于x的方程的两个根；
    （2）判断这两个m是否都正确；如果解题错误，请找出错误原因．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．先化简，再求值：（x+2y）（x-2y）-[-2xy（2x2+3y2）+8x3y]÷2xy，其中|x+1|+（y-$\frac{\sqrt{3}}{3}$）2014=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列性质中正方形具有而其它菱形没有的是（　　）
    A．对角线互相平分B．四条边都相等C．对角线互相垂直D．四个角都是直角

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列字母中，绕某点旋转180°后，不能与原来重合的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．阅读下面材料，并解答下列各题：
    在形如ab=N的式子中，我们已经研究过两种情况：
    ①已知a和b，求N，这是乘方运算；
    ②已知b和N，求a，这是开方运算；
    现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算．
    定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记着b=logaN．
    例如：因为23=8，所以log28=3；因为2-3=$\frac{1}{8}$，所以log2$\frac{1}{8}$=-3．
    （1）根据定义计算：
    ①log381=4；②log33=1；
    ③如果logx16=4，那么x=2．
    （2）设ax=M，ay=N，则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），
    ∵ax•ay=ax+y，∴ax+y=M•N∴logaMN=x+y，
    即logaMN=logaM+logaN
    这是对数运算的重要性质之一，进一步，我们还可以得出：logaM1M2M3…Mn=logaM1+logaM2+…+logaMn
    （其中M1、M2、M3、…、Mn均为正数，a＞0，a≠1）loga$\frac{M}{N}$=logaM-logaN（a＞0，a≠1，M、N均为正数）．

    查看答案和解析>>

    同步练习册答案