
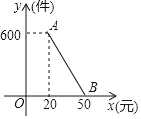
【题目】某网商经销一种畅销玩具,每件进价为18元,每月销量y(件)与销售单价x(元)之间的函数关系如图中线段AB所示
(Ⅰ)写出毎月销量y(件)与销售单价x(元)之间的函数关系式(含x的取值范围) ;
(Ⅱ)当销售单价为多少元时,该网商毎月经销这种玩具能够获得最大销售利润?最大销售利润是多少?(销售利润=售价﹣进价)
【答案】(1)y=﹣20x+1000(20≤x≤50)(2)当销售单价为34元时,该网商每月经销这种玩具能够获得最大销售利润,最大销售利润是5120元
【解析】
(1)根据函数图象中的数据可以求得线段AB对应的函数解析式;
(2)利用(1)所求可以得到利润和售价之间的函数关系式,然后根据二次函数的性质即可解答本题.
(1)设AB段对应的函数解析式为y=kx+b,
![]() ,
,
解得:![]() ,
,
即AB段对应的函数解析式为y=﹣20x+1000(20≤x≤50);
故答案为:y=﹣20x+1000(20≤x≤50);
(2)设销售利润为w元,
w=(x﹣18)(﹣20x+1000)=﹣20x2+1360x﹣18000=﹣20(x﹣34)2+5120,
∵20≤x≤50,
∴当x=34时,w取得最大值,此时w=5120,
答:当销售单价为34元时,该网商每月经销这种玩具能够获得最大销售利润,最大销售利润是5120元.


科目:初中数学 来源: 题型:
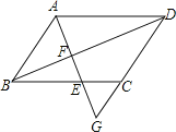
【题目】如图,在平行四边形ABCD中,点G在边DC的延长线上,AG交边BC于点E,交对角线BD于点F.
(1)求证:AF2=EFFG;
(2)如果EF=![]() ,FG=
,FG=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 设![]() 为单位向量,那么
为单位向量,那么![]()
B. 已知![]() 、
、![]() 、
、![]() 都是非零向量,如果
都是非零向量,如果![]() ,
,![]() ,那么
,那么![]()
C. 四边形![]() 中,如果满足
中,如果满足![]() ,
,![]() ,那么这个四边形一定是平行四边形
,那么这个四边形一定是平行四边形
D. 平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解
查看答案和解析>>
科目:初中数学 来源: 题型:
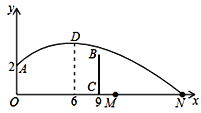
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x![]() k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A. 球不会过网 B. 球会过球网但不会出界
C. 球会过球网并会出界 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,经过正方形ABCD的顶点A在其外侧作直线AP,点B关于直线AP的对称点为E,连接BE、DE,其中DE交直线AP于点F.
(1)依题意补全图1.
(2)若∠PAB=30°,求∠ADF的度数.
(3)如图,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象与x轴交于A(﹣2,0)、B(4,0)两点,且函数经过点(3,10).
(1)求二次函数的解析式;
(2)设这个二次函数的顶点为P,求△ABP的面积;
(3)当x为何值时,y≤0.(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
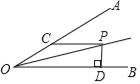
【题目】如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=8,则PD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年,中央全面落实“稳房价”的长效管控机制,重庆房市较上一年大幅降温,11月,LH地产共推出了大平层和小三居两种房型共80套,其中大平层每套面积180平方米,单价1.8万元/平方米,小三居每套面积120平方米,单价1.5万元/平方米.
(1)LH地产11月的销售总额为18720万元,问11月要推出多少套大平层房型?
(2)2019年12月,中央经济会议上重申“房子是拿来住的,不是拿来炒的”,重庆房市成功稳定并略有回落.为年底清盘促销,LH地产调整营销方案,12月推出两种房型的总数量仍为80套,并将大平层的单价在原有基础上每平方米下调![]() 万元(m>0),将小三居的单价在原有基础上每平方米下调
万元(m>0),将小三居的单价在原有基础上每平方米下调![]() 万元,这样大平层的销量较(1)中11月的销量上涨了7m套,且推出的房屋全部售罄,结果12月的销售总额恰好与(1)中I1月的销售总额相等.求出m的值.
万元,这样大平层的销量较(1)中11月的销量上涨了7m套,且推出的房屋全部售罄,结果12月的销售总额恰好与(1)中I1月的销售总额相等.求出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com