
如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.

(1)求证:△EBF∽△FCD;
(2)连接DH,如果BC=12,BF=3,求tan∠HDG的值.
(1)证明见试题解析;(2)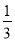 .
.
【解析】
试题分析:(1)由正方形的性质得到∠B=∠C=90°,∠EFG=90°,BC=CD,GH=EF=FG.由∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,得到 ∠EFB =∠FDC.故△EBF∽△FCD;
(2)在Rt△CDF中,由勾股定理得到DF的长,由△EBF∽△FCD,得到 BE的长,再由勾股定理得到GH=的长,由于DG=DF-FG=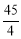 ,故可得到 tan∠HDG的值.
,故可得到 tan∠HDG的值.
试题解析:(1)证明:∵ 正方形ABCD,正方形EFGH,∴ ∠B=∠C=90°,∠EFG=90°,BC=CD,GH=EF=FG.又∵ 点F在BC上,点G在FD上,

 ∴ ∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,∴ ∠EFB =∠FDC.∴ △EBF∽△FCD;
∴ ∠DFC+∠EFB=90°,∠DFC+∠FDC=90°,∴ ∠EFB =∠FDC.∴ △EBF∽△FCD;
(2)【解析】
∵ BF=3,BC=CD=12,
 ∴ CF=9,DF=
∴ CF=9,DF=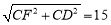 ,由(1)得
,由(1)得 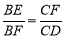 ,∴ BE=
,∴ BE=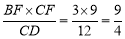 ,∴GH=FG=EF=
,∴GH=FG=EF=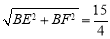 ,DG=DF-FG=
,DG=DF-FG=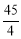 ,∴ tan∠HDG=
,∴ tan∠HDG=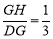 .
.
考点:1.正方形的性质;2.相似三角形的判定与性质;3.解直角三角形.


科目:初中数学 来源:2014-2015学年河南省郑州市九年级第一次质量预测数学试卷(解析版) 题型:解答题
(9分)在信息快速发展的社会,“信息消费”已成为人们生活的重要部分.郑州市的一个社区随机抽取了部分家庭,调查每月用于信息消费的金额,数据整理成如图所示的不完整统计图.已知A、B两组户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.
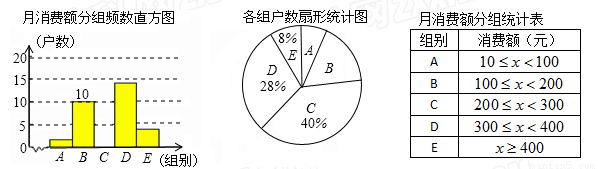
(1)A组的频数是 ,本次调查样本的容量是 ;
(2)补全直方图(需标明各组频数);
(3)若该社区有1500户住户,请估计月信息消费额不少于300元的户数是多少?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市延庆县九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:△ABC是⊙O的内接三角形,AB=AC,在∠BAC所对弧AC上,任取一点D,连接AD,BD,CD,
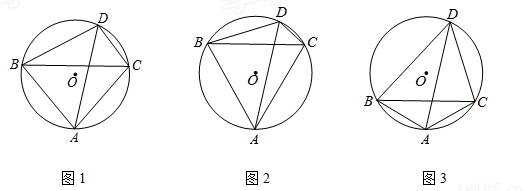
(1)如图1,∠BAC=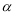 ,直接写出∠ADB的大小(用含
,直接写出∠ADB的大小(用含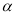 的式子表示);
的式子表示);
(2)如图2,如果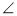 BAC=60°,求证:BD+CD=AD;
BAC=60°,求证:BD+CD=AD;
(3)如图3,如果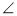 BAC=120°,那么BD+CD与AD之间的数量关系是什么?写出猜测并加以证明.
BAC=120°,那么BD+CD与AD之间的数量关系是什么?写出猜测并加以证明.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市延庆县九年级上学期期末考试数学试卷(解析版) 题型:选择题
二次函数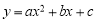 的图象如图所示,则下列结论中错误的是( )
的图象如图所示,则下列结论中错误的是( )
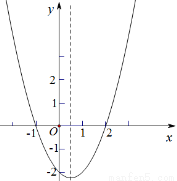
A.函数有最小值
B.当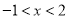 时,
时,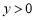
C.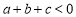
D.当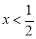 ,y随x的增大而减小
,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图1,对于平面上不大于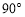 的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为
的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为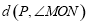 .
.
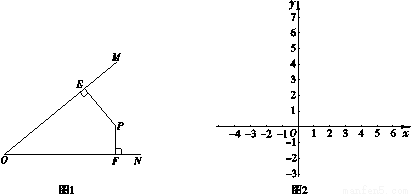
如图2,在平面直角坐标系xOy中,对于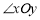 ,点P为第一象限内或两条坐标轴正半轴上的动点,且满足
,点P为第一象限内或两条坐标轴正半轴上的动点,且满足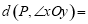 5,点P运动形成的图形记为图形G.
5,点P运动形成的图形记为图形G.
(1)满足条件的其中一个点P的坐标是 ,图形G与坐标轴围成图形的面积等于 ;
(2)设图形G与x轴的公共点为点A,已知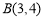 ,
,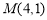 ,求
,求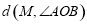 的值;
的值;
(3)如果抛物线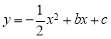 经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当
经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当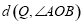 取最大值时,点Q 的坐标.
取最大值时,点Q 的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在⊙O中,点P在直径AB的延长线上,PC,PD与⊙O相切,切点分别为点C,点D,连接CD交AB于点E.如果⊙O的半径等于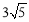 ,tan∠CPO=
,tan∠CPO=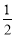 ,求弦CD的长.
,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市西城区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
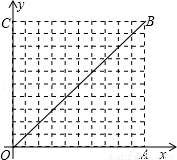
A.16 B.15 C.14 D.13
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省心学校九年级上学期数学试卷(解析版) 题型:填空题
二次函数y=ax2+bx+c的图象如图所示,以下结论:①a+b+c=0;②4a+b=0;③abc<0;④4ac-b2<0;⑤当x≠2时,总有4a+2b>ax2+bx;其中正确的有 (填写正确结论的序号).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川中江县继光实验学校九年级上期末模拟考试数学试卷(解析版) 题型:解答题
如图(1),抛物线 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0,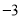 ).[图(2)为解答备用图]
).[图(2)为解答备用图]

(1) __________,点A的坐标为___________,点B的坐标为__________;
__________,点A的坐标为___________,点B的坐标为__________;
(2)设抛物线 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com