
【题目】某中学九年级学生开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度,如图,他们先在点C测得教学楼AB的顶点A的仰角为30°,然后向教学楼前进20米到达点D,又测得点A的仰角为45°,请根据这些数据,求这幢教学楼的高度.(最后结果精确到1米,参考数据 ![]() ≈1.732)
≈1.732) 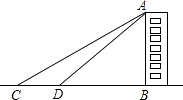
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,则一元二次方程ax2+bx+c=0( ) 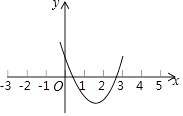
A.没有实根
B.只有一个实根
C.有两个实根,且一根为正,一根为负
D.有两个实根,且一根小于1,一根大于2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )

A. (0,4) B. (0,3) C. (﹣4,0) D. (0,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A是双曲线y= ![]() (x>0)上一点,过点A作AB∥x轴,交双曲线y=﹣
(x>0)上一点,过点A作AB∥x轴,交双曲线y=﹣ ![]() (x<0)于点B,若OA⊥OB,则
(x<0)于点B,若OA⊥OB,则 ![]() 的值为( )
的值为( ) 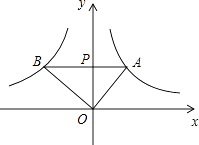
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每小正方形的边长为![]() 个单位,每个小方格的顶点叫格点.
个单位,每个小方格的顶点叫格点.

(1)画出![]() 的
的![]() 边上的中线
边上的中线![]() ;
;
(2)画出![]() 向右平移
向右平移![]() 个单位后得到的
个单位后得到的![]() ;
;
(3)图中![]() 与
与![]() 的关系是 ;
的关系是 ;
(4)能使![]() 的格点
的格点![]() (不同于点
(不同于点![]() ),共有 个,在图中分别用
),共有 个,在图中分别用![]() 、
、![]() 、
、![]() 表示出来.
表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
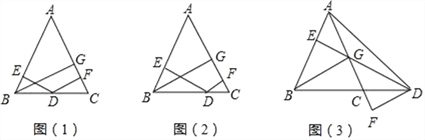
【题目】如图,在△ABC中,AB=AC,BG⊥AC于G,DE⊥AB于E,DF⊥AC于F.
(1)在图(1)中,D是BC边上的中点,判断DE+DF和BG的关系,并说明理由.
(2)在图(2)中,D是线段BC上的任意一点,DE+DF和BG的关系是否仍然成立?如果成立,证明你的结论;如果不成立,请说明理由.
(3)在图(3)中,D是线段BC延长线上的点,探究DE、DF与BG的关系.(不要求证明,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】著名的瑞士数学家欧拉曾指出:可以表示为四个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为四个整数平方之和,即![]()
![]() ,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
,这就是著名的欧拉恒等式,有人称这样的数为“不变心的数”.实际上,上述结论可减弱为:可以表示为两个整数平方之和的甲、乙两数相乘,其乘积仍然可以表示为两个整数平方之和.
【动手一试】
试将![]() 改成两个整数平方之和的形式.
改成两个整数平方之和的形式. ![]() ;
;
【阅读思考】
在数学思想中,有种解题技巧称之为“无中生有”.例如问题:将代数式![]() 改成两个平方之差的形式.解:原式
改成两个平方之差的形式.解:原式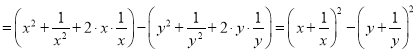 ﹒
﹒
【解决问题】
请你灵活运用利用上述思想来解决“不变心的数”问题:将代数式![]() 改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
改成两个整数平方之和的形式(其中a、b、c、d均为整数),并给出详细的推导过程﹒
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com