
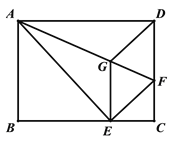
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2)若AG=7、GF=3,求DF的长.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接DE交AF于H,先根据DF=EG,DF∥EG,判定四边形DFEG是平行四边形,再根据GF⊥DE,即可得出四边形EFDG是菱形;
(2)根据条件得到FH=![]() GF=
GF=![]() ,AF=10,再根据Rt△ADF中,DH⊥AF,运用射影定理即可得到DF2=FH×FA,进而得出DF的长.
,AF=10,再根据Rt△ADF中,DH⊥AF,运用射影定理即可得到DF2=FH×FA,进而得出DF的长.
试题解析: (1)如图,连接DE交AF于H,
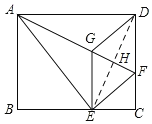
由折叠可得,AF⊥DE,DF=EF,∠DFG=∠EFG,
∵EG∥CD,
∴∠DFG=∠EGF,
∴∠EFG=∠EGF,
∴EG=EF,
∴DF=EG,
∵DF∥EG,
∴四边形DFEG是平行四边形,
∵GF⊥DE,
∴四边形EFDG是菱形;
(2)∵四边形EFDG是菱形,
∴FH=![]() GF=
GF=![]() ,
,
∵AG=7,GF=3,
∴AF=10,
∵Rt△ADF中,DH⊥AF,
∴DF2=FH×FA,
即DF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
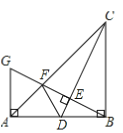
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D是线段AB上的一点,连接CD,过点B作BG⊥CD,分别交CD,CA于点E,F,与过点A且垂直于AB的直线相交于点G,连接DF.给出以下四个结论:①![]() ②若点D是AB的中点,则AF=
②若点D是AB的中点,则AF=![]() AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若
AB;③当B,C,F,D四点在同一个圆上时,DF=DB;④若![]() ,则
,则![]() ,其中正确的结论序号是( )
,其中正确的结论序号是( )
A. ①② B. ③④ C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
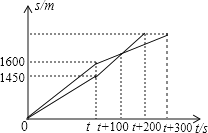
【题目】在一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m,此后两人分别调整速度,并以各自新的速度匀速跑,又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.他们赛跑使用时间t(s)及所跑距离如图s(m),这次越野赛的赛跑全程为 m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017山东省菏泽市,第20题,7分)如图,一次函数y=kx+b与反比例函数![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年8月连淮扬镇铁路正式通车,高邮迈入高铁时代,动车的平均速度为![]() (动车的长度不计),高铁的平均速度为
(动车的长度不计),高铁的平均速度为![]() (高铁的长度不计),扬州市内依次设有6个站点,宝应站、高邮北站、高邮高铁站、邵伯站、江都站、扬州高铁站,假设每两个相邻站点之间的路程都相等,已知一列动车、一列高铁同时经过宝应站开往扬州高铁站,若中途不停靠任何站点,到达扬州高铁站时高铁比动车将早到10分钟
(高铁的长度不计),扬州市内依次设有6个站点,宝应站、高邮北站、高邮高铁站、邵伯站、江都站、扬州高铁站,假设每两个相邻站点之间的路程都相等,已知一列动车、一列高铁同时经过宝应站开往扬州高铁站,若中途不停靠任何站点,到达扬州高铁站时高铁比动车将早到10分钟
(1)求宝应站到扬州高铁站的路程;
(2)若一列动车6:00从宝应站出发,每个站点都停靠4分钟,一列高铁6:18从宝应站出发,只停靠高邮北站、江都站,每个站点都停靠4分钟.
①求高铁经过多长时间追上动车;
②求高铁经过多长时间后,与动车的距离相距20千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数![]() ,B点示数
,B点示数![]() ,C点表示数
,C点表示数![]() ,
,![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() .
.
![]()
(1)![]() =__________,
=__________,![]() =__________,
=__________,![]() =__________;
=__________;
(2)若将数轴折叠,使得A点与C点重合,则点B与数__________表示的点重合;
(3)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动,假设![]() 秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求
秒钟过后,A、B、C三点中恰有一点为另外两点的中点,求![]() 的值;
的值;
(4)若点A、点B和点C分别以每秒2个单位、1个单位长度和4个单位长度的速度在数轴上同时向左运动时,小聪同学发现:当点C在B点右侧时,![]() BC+3AB的值是个定值,求此时
BC+3AB的值是个定值,求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
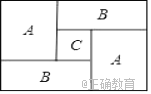
【题目】如图,一个长方形运动场被分隔成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共
共![]() 个区,
个区, ![]() 区是边长为
区是边长为![]() 的正方形,
的正方形, ![]() 区是边长为
区是边长为![]() 的正方形.
的正方形.
(1)列式表示每个![]() 区长方形场地的周长,并将式子化简;
区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果![]() ,
, ![]() ,求整个长方形运动场的面积.
,求整个长方形运动场的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两城相距900千米,一辆客车从A城开往B城,车速为每小时80千米,同时一辆出租车从B城开往A城,车速为每小时100千米,设客车出发时间为t(小时).
探究 若客车、出租车距A城的距离分别为y1、y2,写出y1、y2关于t的函数关系式及自变量取值范围,并计算当y1=240千米时y2的値.
发现 (1)设点C是A城与B城的中点,AC=![]() AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
AB,通过计算说明:哪个车先到达C城?该车到达C后再经过多少小时,另一个车会到达C?
(2)若两车扣相距100千米时,求时间t.
决策 已知客车和出租车正好在A,B之间的服务站D处相遇,此时出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种选择返回B城的方案:
方案一:继续乘坐出租车到C城,加油后立刻返回B城,出租车加油时间忽略不计;
方案二:在D处换乘客车返回B城.
试通过计算,分析小王选择哪种方式能更快到达B城?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com