
【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
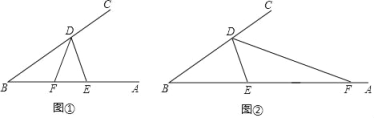
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.
【答案】(1)见解析;(2)EF=DE+BD,证明见解析.
【解析】
(1)如图①,在BA上截取EG=DE,连接DG,得到∠EDG=∠EGD,根据三角形外角的性质和角平分线的定义即可得到结论;
(2)在BA上截取EG=DE,连接DG,则∠EDG=∠EGD,根据三角形外角的性质和角平分线的定义即可得到结论.
(1)如图①,在BA上截取EG=DE,连接DG,
则∠EDG=∠EGD,
∵∠DEB=∠EDG+∠EGD=2∠EGD,
∵∠DEB=2∠B,
∴∠B=∠DGB,
∴BD=DG,
∵DF平分∠BDE,
∴∠BDF=∠EDF,
∵∠DFE=∠B+∠BDF,∠FDG=∠FDE+∠EDG,
∴∠DFG=∠FDG,
∴DG=GF,
∴FG=BD,
∵FG=EF+AE,
∴BD=DE+EF;
(2)如图②在BA上截取EG=DE,连接DG,
则∠EDG=∠EGD,
∵∠DEB=∠EDG+∠EGD=2∠EGD,
∵∠DEB=2∠B,
∴∠B=∠DGB,
∴BD=DG,
∵DF平分∠CDE,
∴∠CDF=∠EDF,
∵∠DFE=∠CDF﹣∠B,∠GDF=∠EDF﹣∠EDG,
∴∠GDF=∠DFG,
∴DG=FG,
∴GF=BD,
∵EF=EG+GF,
∴EF=DE+BD.



 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,∠C=72°,点D在AC上,BC=BD,DE∥BC交AB于点E,则图中等腰三角形共有( )

A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2_______∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2=______.
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°- = ,猜想∠BDA+∠CEA与∠A的关系为

查看答案和解析>>
科目:初中数学 来源: 题型:
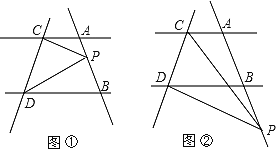
【题目】如图,已知直线AC∥BD,直线AB、CD不平行,点P在直线AB上,且和点A、B不重合.
(1)如图①,当点P在线段AB上时,若∠PCA=20°,∠PDB=30°,求∠CPD的度数;
(2)点P在A、B两点之间运动时,∠PCA、∠PDB、∠CPD之间满足什么样的等量关系(直接写出答案);
(3)如图②,当点P在线段AB的延长线上运动时,∠PCA、∠PDB、∠CPD之间满足什么样的等量关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是
是![]() 的中点;过点
的中点;过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
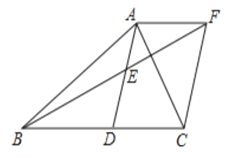
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 分别满足什么条件时,四边形
分别满足什么条件时,四边形![]() 是菱形;四边形
是菱形;四边形![]() 是矩形,并说明理由.
是矩形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=![]() ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.
,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系中,点A(o,m),点B(n,0),m, n满足![]() .
.
(1)求A,B的坐标.
(2)如图1, E为第二象限内直线AB上的一点,且满足![]() ,求点E的横坐标.
,求点E的横坐标.
(3)如图2,平移线段BA至OC, B与O是对应点,A与C是对应点,连接AC, E为BA的延长线上一点,连接EO, OF平分∠COE, AF平分∠EAC, OF交AF于点F,若∠ABO+∠OEB=α,请在图2中将图形补充完整,并求∠F (用含α的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com