
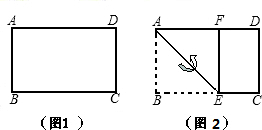
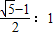 的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.
的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |


| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
如图,把一张标准纸一次又一次对开,得到“2开”纸,“4开”纸,“8开”纸,“16开”纸….已知标准纸的短边长为a.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
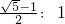 的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.
的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.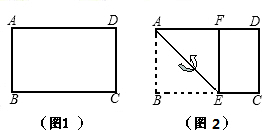
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com