
在某张航海图上,标明了三个观测点的坐标,如图所示,O(0,0)、B(6,0)、C(6、8),由三个观测点确定的图形区域是海洋生物保护区.
(1)求圆形区域的面积(p 取3.14);
(2)某时刻海面上出现一渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离( ,保留三个有效数字);
,保留三个有效数字);
(3)当渔船A由(2)中位置向正西方向航行时,是否进入海洋生物保护区?通过计算回答.

|
(1) 连接CB、CO,则CB∥y轴,∴∠ CBO=90°.设 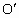 为则O、B、C三点所确定圆的圆心,则OC为 为则O、B、C三点所确定圆的圆心,则OC为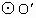 的直径. 的直径.
由已知得, OB=6,CB=8,由勾股定理得,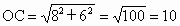 . .
半径 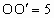 , ,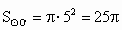 . .
(2) 根据题意可画图,过点A作AD⊥x轴于点D.∠ AOD=45°,∠BAD=30°,∠ABD=90°-30°=60°,设BD=x,则 AB=2x,在Rt△ABD中,由勾股定理得,
由题意知: OD=OB+BD=6+x.在Rt△AOD中,OD=AD,∴ 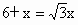 ,即1.7x-x=6. ,即1.7x-x=6.
解得  ,∴ ,∴ . .
(3) 过点A作AG⊥y轴于点G,过点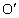 作 作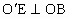 于E,并延长 于E,并延长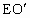 交AG于点F. 交AG于点F.
由 (1)知,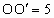 ,∴ ,∴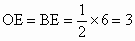 . .
∴在 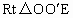 中, 中, . .
∴四边形 FEDA为矩形.∴ EF=DA,而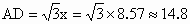 . .
∴ 
∴直线 AG与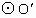 相离,A船不会进入海洋生物保护区. 相离,A船不会进入海洋生物保护区.
|


科目:初中数学 来源: 题型:
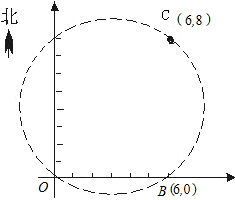 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
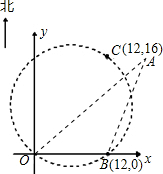 在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是海洋生物保护区,如图所示.
在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是海洋生物保护区,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
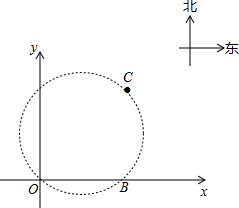 (2011•太原二模)在某张航海图上,标明了三个观测站的坐标,它们分别是O(0,0)、B(6,0)和C(6,8),由这三个站点确定的圆形区域是海洋生物保护区.
(2011•太原二模)在某张航海图上,标明了三个观测站的坐标,它们分别是O(0,0)、B(6,0)和C(6,8),由这三个站点确定的圆形区域是海洋生物保护区.查看答案和解析>>
科目:初中数学 来源:2010-2011学年福建莆田秀屿区实验中学中考模拟数学试卷 题型:解答题
在某张航海图上,标明了三个观测点的坐标为O(0,0)、B(12,0)、C(12,16),由三个观测点确定的圆形区域是海洋生物保护区,如图所示

1.求圆形区域的面积( 取3.14);
取3.14);
2.某时刻海面上出现一渔船A,在观测点O测得A位于北偏东45°方向上,同时在观测点B测得A位于北偏东30°方向上,求观测点B到渔船A的距离(结果保留三个有效数字)
3.当渔船A由(2)中的位置向正西方向航行时,是否会进入海洋生物保护区?请通过计算解释.
查看答案和解析>>
科目:初中数学 来源:第1章《解直角三角形》常考题集(18):1.3 解直角三角形(解析版) 题型:解答题
 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区. ≈1.7,保留三个有效数字);
≈1.7,保留三个有效数字);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com