
分析 先确定两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线,于是可根据此规律得到平面上不同的8个点最多可确定(1+2+3+4+5+6+7)=28条直线.
解答 解:两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线,
因为1+2+3+4+5+6+7=28,
所以平面上不同的8个点最多可确定28条直线.
故答案是:8.
点评 本题考查了直线、射线、线段:直线用一个小写字母表示,如:直线l,或用两个大写字母(直线上的)表示,如直线AB;射线是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边;线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
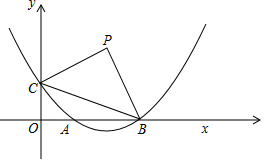 已知:如图,在平面直角坐标系xOy中,抛物线y=ax2-4ax+1与x轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.
已知:如图,在平面直角坐标系xOy中,抛物线y=ax2-4ax+1与x轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
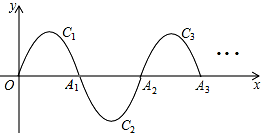 如图,一条抛物线y=-x(x-2)(0≤x≤2)的一部分,记为C1,它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2,交x轴于点A2,;将C2绕点A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(2017,y)在抛物线Cn上,则y=1.
如图,一条抛物线y=-x(x-2)(0≤x≤2)的一部分,记为C1,它与x轴交于O,A1两点,将C1绕点A1旋转180°得到C2,交x轴于点A2,;将C2绕点A2旋转180°得到C3,交x轴于A3;…如此进行下去,直至得到C6,若点P(2017,y)在抛物线Cn上,则y=1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
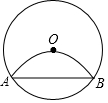 如图,线段AB是⊙O的弦,点P在⊙O上(点P不与点A、点B重合),连接AP、BP,若将⊙O沿弦AB折叠,圆弧恰好经过圆心O,则∠APB的大小为60°或120度.
如图,线段AB是⊙O的弦,点P在⊙O上(点P不与点A、点B重合),连接AP、BP,若将⊙O沿弦AB折叠,圆弧恰好经过圆心O,则∠APB的大小为60°或120度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 扇面用于写字作画,是我国古代书法、绘画特有的形式之一,扇面一般都是由两个半径不同的同心圆按照一定的圆心角裁剪而成,如图,此扇面的圆心角是120°,大扇形的半径为20cm,小扇形的半径为5cm,则这个扇面的面积是125cm2.
扇面用于写字作画,是我国古代书法、绘画特有的形式之一,扇面一般都是由两个半径不同的同心圆按照一定的圆心角裁剪而成,如图,此扇面的圆心角是120°,大扇形的半径为20cm,小扇形的半径为5cm,则这个扇面的面积是125cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com