
【题目】如图,在△ABC中,∠C=90°,BE平分∠ABC,交AC边于点E,ED⊥AB,垂足为D.若△ABC的周长为12,△ADE的周长为6,则BC的长为( )

A. 3 B. 4 C. 5 D. 6
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,A点坐标为(2,4),B点坐标为(﹣3,﹣2),C点坐标为(3,1).
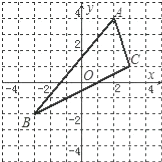
(1)在图中画出△ABC关于y轴对称的△A′B′C′(不写画法),并写出点A′,B′,C′的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一根24cm的筷子置于底面直径为15cm,高为8cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
A. h≤17 B. h≥8 C. 15≤h≤16 D. 7≤h≤16
查看答案和解析>>
科目:初中数学 来源: 题型:
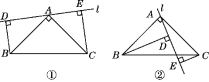
【题目】如图①,在Rt△ABC中,AB=AC,∠BAC=90°,过点A的直线l绕点A旋转,BD⊥l于D,CE⊥l于E.
(1)试说明:DE=BD+CE.
(2)当直线l绕点A旋转到如图②所示的位置时,(1)中结论是否成立?若成立,请说明;若不成立,请探究DE,BD,CE又有怎样的数量关系,并写出探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读材料,再尝试解决问题:
完全平方式![]() 以及
以及![]() 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求![]() 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
解:原式 = ![]() .
.
因为无论![]() 取什么数,都有
取什么数,都有![]() 的值为非负数,所以
的值为非负数,所以![]() 的最小值为0;此时
的最小值为0;此时![]() 时,进而
时,进而![]() 的最小值是
的最小值是![]() ;所以当
;所以当![]() 时,原多项式的最小值是
时,原多项式的最小值是![]() .
.
请根据上面的解题思路,探求:
⑴.多项式![]() 的最小值是多少,并写出对应的
的最小值是多少,并写出对应的![]() 的取值;
的取值;
⑵.多项式![]() 的最大值是多少,并写出对应的
的最大值是多少,并写出对应的![]() 的取值.
的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写推理理由,将过程补充完整:
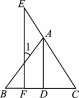
如图,已知AD⊥BC于点D,EF⊥BC于点F,AD平分∠BAC.求证:∠E=∠1.
证明:∵AD⊥BC,EF⊥BC(已知),
∴∠ADC=∠EFC=90°(垂直的定义).
∴____________(_____________).
∴∠1=_____(_____________),
∠E=_____(_______________).
又∵AD平分∠BAC(已知),
∴_____=________.
∴∠1=∠E(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
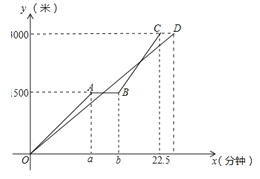
【题目】(2017黑龙江省齐齐哈尔市,第25题,10分)“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人再次选择自行车作为出行工具,小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a= ,b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发至到达图书馆前,何时与小军相距100米?
(4)若小军的行驶速度是v米/分,且在途中与爸爸恰好相遇两次(不包括家、图书馆两地),请直接写出v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.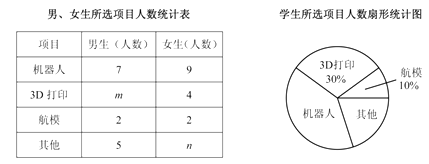
根据以上信息解决下列问题:
(1)![]() ,
, ![]() ;
;![]()
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的 ![]() 名学生中随机选取
名学生中随机选取 ![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的 ![]() 名学生中恰好有
名学生中恰好有 ![]() 名男生、
名男生、 ![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com