
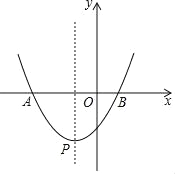
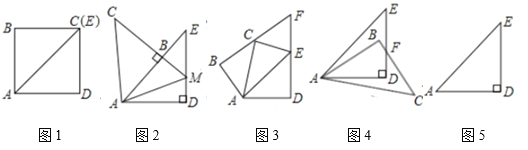
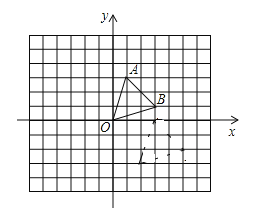
����Ŀ����ͼ��������y=ax2+bx+c��x���ཻ�ڵ�A����3��0����B��1��0������y���ཻ�ڣ�0����![]() ��������ΪP��
��������ΪP��
��1���������߽���ʽ��
��2�����������Ƿ���ڵ�E��ʹ��ABP��������ڡ�ABE������������ڣ�������������ĵ�E�����ꣻ�������ڣ���˵�����ɣ�
��3������ƽ�����Ƿ���ڵ�F��ʹ����A��B��P��FΪ������ı���Ϊƽ���ı��Σ�ֱ��д�����з��������ĵ�F�����꣬�����ƽ���ı��ε������
���𰸡���1��y=![]() x2+x��
x2+x��![]() ��2������������1��2
��2������������1��2![]() ��2����1+2
��2����1+2![]() ��2����3����F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ 8
��2����3����F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ 8
��������
��1���������߽���ʽΪy=ax2+bx+c��������3��0������1��0������0��![]() ���������a��b��c��ֵ���ɣ���2�����������߽���ʽ��֪����P�����꣬�����������εĵ���ͬ�ɵ�Ҫʹ���������������������ȣ�����P�������֪E�������꣬�������ʽ���x��ֵ���ɣ���3���ֱ�����ABΪ�ߡ�ABΪ�Խ�������������F�����겢���������ɣ�
���������a��b��c��ֵ���ɣ���2�����������߽���ʽ��֪����P�����꣬�����������εĵ���ͬ�ɵ�Ҫʹ���������������������ȣ�����P�������֪E�������꣬�������ʽ���x��ֵ���ɣ���3���ֱ�����ABΪ�ߡ�ABΪ�Խ�������������F�����겢���������ɣ�
��1���������߽���ʽΪy=ax2+bx+c��������3��0������1��0������0��![]() �����������߽���ʽ��
�����������߽���ʽ�� ��
��
��ã�a=![]() ��b=1��c=��
��b=1��c=��![]()
�������߽���ʽ��y=![]() x2+x��
x2+x��![]()
��2�����ڣ�
��y=![]() x2+x��
x2+x��![]() =
=![]() ��x+1��2��2
��x+1��2��2
��P����������1����2��
�ߡ�ABP��������ڡ�ABE�������
���E��AB�ľ������2��
��E��a��2����
��![]() a2+a��
a2+a��![]() =2
=2
���a1=��1��2![]() ��a2=��1+2
��a2=��1+2![]()
����������ĵ�E������Ϊ����1��2![]() ��2����1+2
��2����1+2![]() ��2��
��2��
��3���ߵ�A����3��0������B��1��0����
��AB=4
��ABΪ�ߣ�����A��B��P��FΪ������ı���Ϊƽ���ı���
��AB��PF��AB=PF=4
�ߵ�P���꣨��1����2��
���F������3����2��������5����2��
��ƽ���ı��ε����=4��2=8
��ABΪ�Խ��ߣ���A��B��P��FΪ������ı���Ϊƽ���ı���
��AB��PF����ƽ��
���F��x��y���ҵ�A����3��0������B��1��0������P����1����2��
��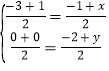 ��
��
��x=��1��y=2
���F����1��2��
��ƽ���ı��ε����=![]() ��4��4=8
��4��4=8
������������F������Ϊ����1��2������3����2��������5����2������ƽ���ı��ε����Ϊ8��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ�����У��Խ̲��е�һ����Ȥ����������̽����

��ϰ��عˣ���֪����ͼ1����![]() �У�
��![]() ��
��![]() �ǽ�ƽ���ߣ�
�ǽ�ƽ���ߣ�![]() �Ǹߣ�
�Ǹߣ�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() .��֤��
.��֤��![]() ��
��
����ʽ˼������ͼ2����![]() �У�
��![]() ��
��![]() ��
��![]() ���ϵĸߣ���
���ϵĸߣ���![]() �����
�����![]() ��ƽ���߽�
��ƽ���߽�![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ���䷴���ӳ�����
���䷴���ӳ�����![]() �ߵ��ӳ��߽��ڵ�
�ߵ��ӳ��߽��ڵ�![]() ����
����![]() ��
��![]() �������˵�����ɣ�
�������˵�����ɣ�
��̽�����죩��ͼ3����![]() �У�
�У�![]() �ϴ���һ��
�ϴ���һ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��ƽ����
��ƽ����![]() ��
��![]() �ڵ�
�ڵ�![]() .
.![]() �����
�����![]() ��ƽ��������ֱ��
��ƽ��������ֱ��![]() ��
��![]() ���ӳ��߽��ڵ�
���ӳ��߽��ڵ�![]() .ֱ��д��
.ֱ��д��![]() ��
��![]() ��������ϵ.
��������ϵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ü������������н����һ���ƽ�ȫ���������С� �����������еĴ���������ѧУ����˫���������������룬��֯������������֪ʶ������ÿ������ͬ������ѧ���μӣ��ɼ��ֱ�Ϊ![]() �ĸ��ȼ�.������Ӧ�ȼ��ĵ÷����μ�Ϊ
�ĸ��ȼ�.������Ӧ�ȼ��ĵ÷����μ�Ϊ![]() �֡�
�֡�![]() �֡�
�֡�![]() �֡�
�֡�![]() �֣�ѧУ�����꼶��һ��Ͷ���ijɼ����������Ƴ�����ͳ��ͼ����
�֣�ѧУ�����꼶��һ��Ͷ���ijɼ����������Ƴ�����ͳ��ͼ����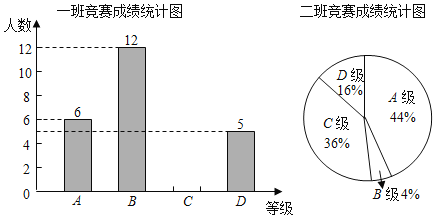
�༶ | ƽ�������֣� | ��λ�����֣� | �������֣� |
һ�� |
|
|
|
���� |
|
|
|
���������ṩ����Ϣ�����������:
(1)�벹ȫһ�ྺ���ɼ�ͳ��ͼ��
(2)��ֱ��д��![]() ��ֵ��
��ֵ��
(3)����Ϊ�ĸ���ɼ��Ϻã���д��֧����۵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ���ó߹���ͼ�ķ�����
���ó߹���ͼ�ķ�����![]() ��ȷ��һ��
��ȷ��һ��![]() ����
����![]() ��������ͼ�����У��������
��������ͼ�����У��������![]() �ij�����ͼ�ǣ� ��
�ij�����ͼ�ǣ� ��
A. B.
B.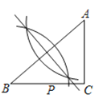 C.
C.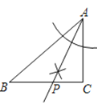 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���Ѷ���С��ͬ��![]() �����ǰ壬�ڷ���ƽ��ֱ������ϵ�У���һ�����ǰ�
�����ǰ壬�ڷ���ƽ��ֱ������ϵ�У���һ�����ǰ�![]() ��һ��ֱ�DZ���
��һ��ֱ�DZ���![]() ���غ��ҵ�
���غ��ҵ�![]() ������Ϊ
������Ϊ![]() ��
��![]() ���ڶ������ǰ��б��
���ڶ������ǰ��б��![]() ���һ�����ǰ��б��
���һ�����ǰ��б��![]() ��ֱ�ҽ�
��ֱ�ҽ�![]() ���ڵ�
���ڵ�![]() �����������ǰ��б��
�����������ǰ��б��![]() ��ڶ������ǰ��б��
��ڶ������ǰ��б��![]() ��ֱ�ҽ�
��ֱ�ҽ�![]() ���ڵ�
���ڵ�![]() �����Ŀ����ǰ�б��
�����Ŀ����ǰ�б��![]() ����������ǰ��б��
����������ǰ��б��![]() ��ֱ�ҽ�
��ֱ�ҽ�![]() ���ڵ�
���ڵ�![]() �����˹��ɼ�����ȥ�����
�����˹��ɼ�����ȥ�����![]() ������Ϊ�� ��
�������� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��龳�����ۺ�ʵ�����ϣ�ͬѧ��̽����ȫ�ȵĵ���ֱ��������ͼ�α仯������
��ͼ1��![]() ������
������![]() ��
��![]() ����ʱ����
����ʱ����![]() ���
���![]() �غϣ�
�غϣ�
����̽��1:��1��С����ͼ1�е�����ȫ�ȵ�![]() ��
��![]() ��ͼ2��ʽ�ڷţ���
��ͼ2��ʽ�ڷţ���![]() ����
����![]() �ϣ�
�ϣ�![]() ����ֱ�߽�
����ֱ�߽�![]() ����ֱ���ڵ�
����ֱ���ڵ�![]() ������
������![]() ����֤��
����֤��![]() ��
��
����̽��2:��2��С��ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת�Ƕ�
����ʱ�뷽����ת�Ƕ�![]()
![]() ��Ȼ�ֱ��ӳ�
��Ȼ�ֱ��ӳ�![]() ��
��![]() �������ཻ�ڵ�
�������ཻ�ڵ�![]() ����ͼ3���ڲ����У�С������������⣬������
����ͼ3���ڲ����У�С������������⣬������
��![]() ʱ����֤��
ʱ����֤��![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�
�ڵ�![]() __________ʱ��
__________ʱ��![]() ����ֱ�ӻشɣ�
����ֱ�ӻشɣ�
����̽��3:��3��Сӱ��ͼ1�е�![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת�Ƕ�
��˳ʱ�뷽����ת�Ƕ�![]()
![]() ���߶�
���߶�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ���ڲ����У�Сӱ����������⣬������
���ڲ����У�Сӱ����������⣬������
����ͼ4����![]() ʱ��ֱ��д���߶�
ʱ��ֱ��д���߶�![]() �ij�Ϊ_________��
�ij�Ϊ_________��
����ͼ5������ת����![]() �DZ�
�DZ�![]() ���е�ʱ��ֱ��д���߶�
���е�ʱ��ֱ��д���߶�![]() �ij�Ϊ____________��
�ij�Ϊ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
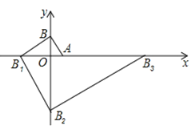
����Ŀ����֪����ƽ���ڵ�������![]() ��
��![]() ��
��![]() ����
����![]() ����ƽ��3����λ������ƽ��2����λ���
����ƽ��3����λ������ƽ��2����λ���![]() .
.
��1������![]() ��
��
��2��![]() �����Ϊ .
�����Ϊ .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
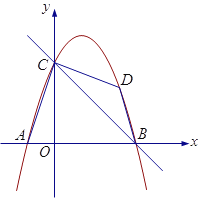
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ��������
��������![]() ������
������![]() ��
��![]() ������
������![]() �����һ����Ϊ
�����һ����Ϊ![]() ������
������![]() .
.
��1���������ߵĽ���ʽ��
��2����![]() ���߶�
���߶�![]() �Ϸ����������ϣ�����
�Ϸ����������ϣ�����![]() ��
��![]() ����
����![]() ��
��![]() �������
�������![]() �����
�����![]() �����ꣻ
�����ꣻ
��3����ͼ2��![]() Ϊ
Ϊ![]() �е㣬��
�е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣨�����˵㣩������
��һ�㣨�����˵㣩������![]() ��һ����
��һ����![]() ��
��![]() ���������߶�
���������߶�![]() ��ÿ��1����λ���ٶ��˶���
��ÿ��1����λ���ٶ��˶���![]() ���������߶�
���������߶�![]() ��ÿ��
��ÿ��![]() ����λ���ٶ��˶���
����λ���ٶ��˶���![]() ��ֹͣ������
��ֹͣ������![]() �������Ƕ���ʱ����
�������Ƕ���ʱ����![]() �������˶���������ʱ���٣�����ʱ���Ǽ��룿
�������˶���������ʱ���٣�����ʱ���Ǽ��룿

ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ������Ҫ��һ�����εIJֿ⣬�ֿ��������ס��ǽ������������![]() ���Ľ�������Χ�ɣ��Ҳֿ�����Ϊ
���Ľ�������Χ�ɣ��Ҳֿ�����Ϊ![]() ��
��
![]() ������βֿ�ij���
������βֿ�ij���
![]() �й��Ϊ
�й��Ϊ![]() ��
��![]() �����
����λ��![]() ���ĵذ�ש���۷ֱ�Ϊ
���ĵذ�ש���۷ֱ�Ϊ![]() Ԫ/���
Ԫ/���![]() Ԫ/�飬��ֻѡ����һ�ֵذ�ש��ǡ���������ֿ�ľ��ε��棨���Ʒ�϶��������һ�ֹ��ĵذ�ש���ý��٣�
Ԫ/�飬��ֻѡ����һ�ֵذ�ש��ǡ���������ֿ�ľ��ε��棨���Ʒ�϶��������һ�ֹ��ĵذ�ש���ý��٣�

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com